题目内容
14.观察下列各式:-1×$\frac{1}{2}$=-1+$\frac{1}{2}$
-$\frac{1}{2}$×$\frac{1}{3}$=-$\frac{1}{2}$+$\frac{1}{3}$
-$\frac{1}{3}$×$\frac{1}{4}$=-$\frac{1}{3}$+$\frac{1}{4}$
(1)你发现的规律是-$\frac{1}{n}$×$\frac{1}{n+1}$=-$\frac{1}{n}$+$\frac{1}{n+1}$.
(2)用规律计算:-1×$\frac{1}{2}$+(-$\frac{1}{2}$×$\frac{1}{3}$)+(-$\frac{1}{3}$×$\frac{1}{4}$ )+…+(-$\frac{1}{2011}$×$\frac{1}{2012}$)
分析 (1)根据给出的例子找出规律即可;
(2)根据(1)中的规律即可得出结论.
解答 解:(1)由题意得,-$\frac{1}{n}$×$\frac{1}{n+1}$=-$\frac{1}{n}$+$\frac{1}{n+1}$.
故答案为:-$\frac{1}{n}$+$\frac{1}{n+1}$;
(2)原式=-1+$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{3}$+$\frac{1}{4}$-$\frac{1}{4}$+$\frac{1}{5}$-…-$\frac{1}{2011}$+$\frac{1}{2012}$
=-1+$\frac{1}{2012}$
=-$\frac{2011}{2012}$.
点评 本题考查的是数字的变化类,根据题意找出规律是解答此题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
4.G20峰会期间,杭州市的注册志愿者达到9.17×105人,则近似数9.17×105的精确度是( )
| A. | 百分位 | B. | 个位 | C. | 千位 | D. | 十万位 |
5.有理数2.645精确到百分位的近似数是( )
| A. | 2.6 | B. | 2.64 | C. | 2.65 | D. | 2.7 |
2.如果x2+10x+__=(x+5)2,横线处填( )
| A. | 5 | B. | 10 | C. | 25 | D. | ±10 |
19.已知M到x轴的距离为1,到y轴的距离为2,且M在第四象限,则点M的坐标为( )
| A. | (1,2) | B. | (-1,-2) | C. | (1,-2) | D. | (2,-1) |
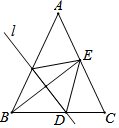 如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.
如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.