题目内容
12．已知P（0，-1），Q（2，0），O为原点，点A和点B在坐标轴上，且△OAB≌△OPQ（点A、B不同时与P、Q重合），求所有满足条件的A、B的坐标．分析 根据P（0，-1），Q（2，0），求得OP=1，OQ=2，根据全等三角形的性质得到OA=OP=1，OB=OQ=2，即可得到结论．
解答 解：∵P（0，-1），Q（2，0），
∴OP=1，OQ=2，
∵△OAB≌△OPQ，
∴OA=OP=1，OB=OQ=2，
∵点A和点B在坐标轴上，
∴A（0，1）或A（0，1），B（-2，0）或B（2，0）．
点评 本题考查了全等三角形的性质，坐标与图形的性质，由△OAB≌△OPQ找好对应关系是解题的关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
17．若平行四边形的对角线和一边垂直，且邻边之比为1：2，则平行四边形的内角中较小的角的大小为（ ）
| A． | 45° | B． | 60° | C． | 30° | D． | 75° |
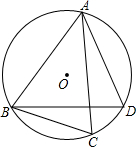如图，已知四边形ABCD是⊙O的内接四边形，连接AC、BD，若AB=AC且∠ABD=60°．求证：AB=BD+CD．
如图，△ABC中，分别以AB、AC为边向外作正方形ABDE、ACFG．试说明：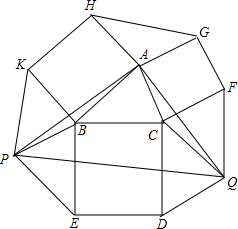
如图，已知△ABC，分别以AB、AC、BC作边作正方形ABKH、正方形ACFG、正方形BCDE，作?BEPK，?CDQF，联结AP，AQ，PQ，求证：△APQ是等腰直角三角形．
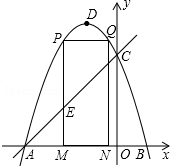如图，抛物线y=-x2-2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．