题目内容
19.观察下列由连续的正整数组成的宝塔形等式:第1层 1+2=3
第2层 4+5+6=7+8
第3层 9+10+11+12=13+14+15
第4层 16+17+18+19+20=21+22+23+24
…
(1)填空:第6层等号右侧的第一个数是43,第n层等号右侧的第一个数是n2+n+1(用含n的式子表示,n是正整数);数字2017排在第几层?请简要说明理由;
(2)求第99层右侧最后三个数字的和.
分析 (1)由题意知,第6层等号左侧的第一个数是62=36、第n层等号左侧的第一个数是n2,分别加上序数加1即可得;根据第n层的第一个数是n2,由442<2016<452可得答案;
(2)由以上规律知第99层右侧最后三个数字为1002-1、1002-2、1002-3,相加可得.
解答 解:(1)由题意知,第6层等号左侧的第一个数是62=36,
∴第6层等号右侧的第一个数是36+6+1=43;
∵第n层等号左侧的第一个数是n2,
∴第n层等号右侧的第一个数是n2+n+1,
由题意知,第n层的第一个数是n2,
∵442=1936,452=2025,
∴442<2017<452,
∴2017排在第44层;
故答案为:43,n2+n+1;44;
(2)由题意知(1002-1)+(1002-2)+(1002-3)
=3×10000-6
=29994,
答:第99层右侧最后三个数字的和为29994.
点评 本题主要考查数字的变化规律,根据题意知第n层的第一个数是n2、第n层的右侧第一个数是n2+n+1是解题的关键.

练习册系列答案
相关题目
 如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.
如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.
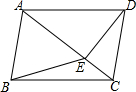 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.