题目内容
11.如图1,正方形ABCD的边长为4厘米,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以每秒a厘米的速度运动,设运动时间为t秒,△PBF的面积记为S.S与t的部分函数图象如图2所示,已知点M(1,$\frac{3}{2}$)、N(5,6)在S与t的函数图象上.(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式,并补全该函数图象;
(3)当t为多少时,△PBF的面积S为4.
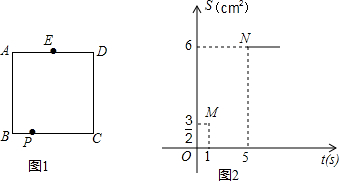
分析 (1)根据t=5时S=6求出BF的长,根据t=1时S=$\frac{3}{2}$列式可计算出a的值;
(2)S与t的函数关系式分以下三种情况:
①点P在BC上运动时,即0≤t≤4;
②点P在CD边上运动,即4<t≤8;
③点P在线段DE上运动时,即8<t≤10,分别按照三角形面积公式列出函数表达式.
(3)把S=4分别代入S=$\frac{3}{2}$t和S=18-$\frac{3}{2}$t,求得t的值即可.
解答 解:(1)根据题意可知,当点P在CD上时,△PBF的面积记为S=6,
则有:$\frac{1}{2}$×BF×4=6,解得:BF=3,
当t=1时,S=$\frac{3}{2}$,BP=a,
则有:$\frac{1}{2}$×BF×BP=$\frac{3}{2}$,即$\frac{1}{2}×3a$=$\frac{3}{2}$,
解得:a=1,
故线段BF的长为3,a的值为1;
(2)当0≤t≤4时,即点P在BC边上运动,
S=$\frac{1}{2}$×BF×BP=$\frac{1}{2}$×3×t=$\frac{3}{2}$t;
当4<t≤8时,即点P在CD边上运动,
此时面积S=$\frac{1}{2}$×BF×BC=$\frac{1}{2}$×3×4=6;
当8<t≤10时,即点P在线段DE上运动,
S=$\frac{1}{2}$×BF×AP=$\frac{1}{2}$×3×(12-t)=18-$\frac{3}{2}$t.
综上:S=$\left\{\begin{array}{l}{\frac{3}{2}t(0≤t≤4)}\\{6(4<t≤8)}\\{18-\frac{3}{2}t(8<t≤10)}\end{array}\right.$;
函数图象如下所示: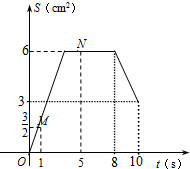
(3)当S=4时,$\frac{3}{2}$t=4,t=$\frac{8}{3}$.
18-$\frac{3}{2}$t=4,t=$\frac{28}{3}$.
故当t=$\frac{8}{3}$或 t=$\frac{28}{3}$时△PBF的面积S为4.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是利用分类讨论的思想求出S与t的函数关系式.

| A. | y2>y1>y3 | B. | y3>y1>y2 | C. | y2>y3>y1 | D. | y1>y3>y2 |
| 自选项目 | 人数 | 频率 |
| 立定跳远 | b | 0.18 |
| 三级蛙跳 | 12 | 0.24 |
| 一分钟跳绳 | 8 | a |
| 投掷实心球 | 16 | 0.32 |
| 推铅球 | 5 | 0.10 |
| 合计 | 50 | 1 |
(2)若该校九年级共有400名学生,试估计年级选择“一分钟跳绳”项目的总人数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.
 如图,CA⊥BE于A,AD∥BC,若∠1=54°,则∠C等于( )
如图,CA⊥BE于A,AD∥BC,若∠1=54°,则∠C等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 54° |
 有理数a,b在数轴上的位置如图所示,则|a+b|等于( )
有理数a,b在数轴上的位置如图所示,则|a+b|等于( )| A. | a+b | B. | b-a | C. | -a-b | D. | 以上都不对 |
 如图,在Rt△ABC中,∠C=90°,AC=$\sqrt{3}$,点D为BC边上一点,且BD=2AD,∠ADC=60°,求BC的长.
如图,在Rt△ABC中,∠C=90°,AC=$\sqrt{3}$,点D为BC边上一点,且BD=2AD,∠ADC=60°,求BC的长. 图中有8块小立方方块,请把它的主视图、左视图和俯视图画出来.
图中有8块小立方方块,请把它的主视图、左视图和俯视图画出来. 如图,为了测量出池塘两端A、B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BD至D,使CD=BC,那么只要测量出AD的长度就得到A,B两点之间的距离,你能说明其中的道理吗?
如图,为了测量出池塘两端A、B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BD至D,使CD=BC,那么只要测量出AD的长度就得到A,B两点之间的距离,你能说明其中的道理吗?