题目内容
16. 如图,CA⊥BE于A,AD∥BC,若∠1=54°,则∠C等于( )
如图,CA⊥BE于A,AD∥BC,若∠1=54°,则∠C等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 54° |
分析 先根据平行线的性质求出∠B的度数,再由垂直的定义得出∠BAC的度数,根据直角三角形的性质即可得出结论.
解答 解:∵AD∥BC,∠1=54°,
∴∠B=∠1=54°.
∵CA⊥BE于A,
∴∠BAC=90°,
∴∠C=90°-∠B=90°-54°=36°.
故选B.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
7.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时第一步应先假设( )
| A. | 每一个内角都大于60° | B. | 至多有一个内角大于60° | ||
| C. | 每一个内角小于或等于60° | D. | 至多有一个内角大于或等于60° |
4.在Rt△ABC中,∠C=90°,BC=1,AC=$\sqrt{3}$,则下列结论中,正确的是( )
| A. | sinA=$\frac{\sqrt{3}}{2}$ | B. | tanA=$\frac{\sqrt{3}}{3}$ | C. | cosB=$\frac{\sqrt{3}}{2}$ | D. | tanB=$\frac{\sqrt{3}}{3}$ |
1. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( )
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( )
 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( )
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( )| A. | $\frac{2}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{5}{7}$ |
6. 如图,在?ABCD中,AB=5,对角线交于点O,△OCD的周长为23,则?ABCD的两条对角线长的和是( )
如图,在?ABCD中,AB=5,对角线交于点O,△OCD的周长为23,则?ABCD的两条对角线长的和是( )
 如图,在?ABCD中,AB=5,对角线交于点O,△OCD的周长为23,则?ABCD的两条对角线长的和是( )
如图,在?ABCD中,AB=5,对角线交于点O,△OCD的周长为23,则?ABCD的两条对角线长的和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
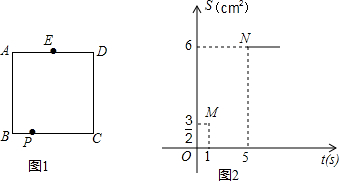
 如图,E是正方形ABCD中CD边上一点,以点A为中心把△ADE顺时针旋转90°.
如图,E是正方形ABCD中CD边上一点,以点A为中心把△ADE顺时针旋转90°.