题目内容
17.如图,将边长为6的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分为菱形时,则AA′为12-6$\sqrt{2}$.
分析 利用菱形的性质结合正方形的性质得出A′D=DF,AA′=A′E,进而利用勾股定理得出答案.
解答 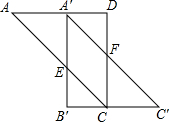 解:如图所示:∵四边形A′ECF是菱形,
解:如图所示:∵四边形A′ECF是菱形,
∴A′E=EC=FC=A′F,
∵边长为6的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,
∴∠A=∠ACD=45°,
∴AD=DC,则A′D=DF,AA′=A′E,
∴设A′E=x,则A′D=DF=6-x,A′F=x,
故在Rt△A′DF中,
x2=(6-x)2+(6-x)2,
解得:x1=12-6$\sqrt{2}$,x2=12+6$\sqrt{2}$>6(不合题意舍去),
故AA′为:12-6$\sqrt{2}$.
故答案为:12-6$\sqrt{2}$.
点评 此题主要考查了菱形的性质和正方形的性质、勾股定理等知识,得出A′D=DF,AA′=A′E是解题关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
8. 如图,AB,CD是⊙O中两条互相垂直的直径,点E在⊙O上,则∠BEC=( )
如图,AB,CD是⊙O中两条互相垂直的直径,点E在⊙O上,则∠BEC=( )
 如图,AB,CD是⊙O中两条互相垂直的直径,点E在⊙O上,则∠BEC=( )
如图,AB,CD是⊙O中两条互相垂直的直径,点E在⊙O上,则∠BEC=( )| A. | 30° | B. | 35° | C. | 45° | D. | 60° |
18.下列正多边形中,不能够铺满地面的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 正六边形 | D. | 正八边形 |
19.下列式子是分式的是( )
| A. | $\frac{x}{2}$ | B. | $\frac{3}{x+1}$ | C. | $\frac{x}{2}+y$ | D. | $\frac{x}{π}$ |
 如图,在正方形ABCD中,延长BC至E,使CE=CA,则∠CAE的度数是22.5度.
如图,在正方形ABCD中,延长BC至E,使CE=CA,则∠CAE的度数是22.5度.