题目内容
15．当（2a+1+2b）（2a-1+2b）=63，a+b=±4．分析 将（2a+2b）看作一个整体，然后利用平方差公式进行计算求出（2a+2b）2，再求解即可．
解答 解：∵（2a+1+2b）（2a-1+2b）
=[（2a+2b）+1][（2a+2b）-1]
=（2a+2b）2-1，
∴（2a+2b）2-1=63，
∴（2a+2b）2=64，
即4（a+b）2=64，
∴（a+b）2=16，
∴a+b=±4．
故答案为：±4．
点评 本题考查了平方差公式，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方，本题要注意整体思想的利用．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
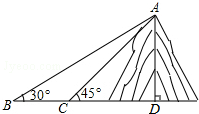如图，小明在一块平地上测山高，先在B处测得山顶A的仰角为30°，然后向山脚直行100米到达C处，再测得山顶A的仰角为45°，求山高AD是多少？（结果保留整数，测角仪忽略不计，参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.73）
a、b、c三点在数轴上的位置如图所示，化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$．
20．设P=a2（-a+b-c），Q=-a（a2-ab+ac），则P与Q的关系是（ ）
| A． | P=Q | B． | P＞Q | C． | P＜Q | D． | 互为相反数 |