题目内容
11.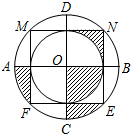 如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.
如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.
分析 由于图形是中心对称图形,则利用旋转把图中阴影部分可整合为扇形OBC,然后根据扇形的面积公式求出图中阴影部分的面积,最后根据概率公式即可得出答案.
解答 解:∵小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,
∴图形是中心对称图形,大圆的半径为$\sqrt{2}$,
∴图中阴影部分的面积=S扇形OBC=$\frac{90•π•(\sqrt{2})^{2}}{360}$=$\frac{1}{2}$π,大圆的面积是:($\sqrt{2}$)2•π=2π,
∴小球停在该图中阴影部分区域的概率为$\frac{\frac{1}{2}π}{2π}$=$\frac{1}{4}$;
故答案为:$\frac{1}{4}$.
点评 本题考查了几何概率,用到的知识点为:概率=相应的面积与总面积之比,关键是根据圆面积公式求出阴影部分的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.2017年3月5日,十二届全国人大五次会议顺利召开,李克强总理在政府工作报告中指出,2016年国内生产总值达到74.4亿元,比上年增长6.7%,将74.4万亿用科学记数法表示是( )
| A. | 7.44×104 | B. | 7.44×108 | C. | 74.4×1012 | D. | 7.44×1013 |
20.已知m>1,则关于x的一元二次方程x2-2x+$\frac{1}{4}$m+3=0根的情况为( )
| A. | 无实数根 | B. | 有两个相等实数根 | ||
| C. | 有两个不相等实数根 | D. | 无法确定 |
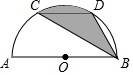 如图,AB是半圆的直径,C、D是$\widehat{AB}$的三分之一点,若半径为R,求阴影部分的面积.
如图,AB是半圆的直径,C、D是$\widehat{AB}$的三分之一点,若半径为R,求阴影部分的面积.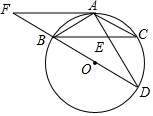 如图,BD为⊙O的直径,AD交BC于点E,AE=2,ED=4,过点A作⊙O的切线FA交DB延长线于点F,且AF∥BC.
如图,BD为⊙O的直径,AD交BC于点E,AE=2,ED=4,过点A作⊙O的切线FA交DB延长线于点F,且AF∥BC.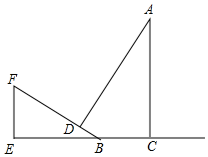 如图,AC时一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,AC时一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是$\frac{8}{3}$π.
如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是$\frac{8}{3}$π. 在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆”
在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆”