题目内容
12. 如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )
如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )| A. | 4 | B. | 3 | C. | 6 | D. | 5 |
分析 过点D作DF⊥AC于F,然后利用△ABC的面积公式列式计算即可得解.
解答  解:过点D作DF⊥AC于F,
解:过点D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,
∴S△ABC=$\frac{1}{2}$×4×2+$\frac{1}{2}$AC×2=7,
解得AC=3.
故选:B.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
2.为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
(1)设从甲仓库运送到A港口的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明费用最低时的调配方案.
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
(2)求出最低费用,并说明费用最低时的调配方案.
20.化简:$\frac{x+3}{x+2}$-$\frac{x-2}{{x}^{2}-4}$=( )
| A. | $\frac{x+4}{x+2}$ | B. | 1 | C. | -1 | D. | $\frac{5}{{x}^{2}-4}$ |
7.-$\sqrt{5}$的绝对值是( )
| A. | -$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
17. 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{EA}=\frac{DF}{AB}$ | B. | $\frac{DE}{BC}=\frac{EF}{FB}$ | C. | $\frac{BC}{DE}=\frac{BF}{BE}$ | D. | $\frac{BF}{BE}=\frac{BC}{AE}$ |
4. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
1.若m1,m2,…m2016是从0,1,2这三个数中取值的一列数,且m1+m2+…+m2016=1546,(m1-1)2+(m2-1)2+…+(m2016-1)2=1510,则在m1,m2,…m2016中,取值为2的个数为( )
| A. | 505 | B. | 510 | C. | 520 | D. | 550 |
2.点(2,-4)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点在此函数图象上的是( )
| A. | (2,4) | B. | (-1,-8) | C. | (-2,-4) | D. | (4,-2) |
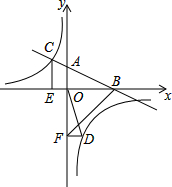 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.