题目内容
3.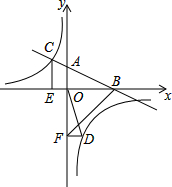 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO,求点D的坐标.
分析 (1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数m,由此即可得出结论;
(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,-$\frac{6}{n}$)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
解答 解:(1)∵OB=4,OE=2,
∴BE=OB+OE=6.
∵CE⊥x轴,
∴∠CEB=90°.
在Rt△BEC中,∠CEB=90°,BE=6,tan∠ABO=$\frac{1}{2}$,
∴CE=BE•tan∠ABO=6×$\frac{1}{2}$=3,
结合函数图象可知点C的坐标为(-2,3).
∵点C在反比例函数y=$\frac{m}{x}$的图象上,
∴m=-2×3=-6,
∴反比例函数的解析式为y=-$\frac{6}{x}$.
(2)∵点D在反比例函数y=-$\frac{6}{x}$第四象限的图象上,
∴设点D的坐标为(n,-$\frac{6}{n}$)(n>0).
在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO=$\frac{1}{2}$,
∴OA=OB•tan∠ABO=4×$\frac{1}{2}$=2.
∵S△BAF=$\frac{1}{2}$AF•OB=$\frac{1}{2}$(OA+OF)•OB=$\frac{1}{2}$(2+$\frac{6}{n}$)×4=4+$\frac{12}{n}$.
∵点D在反比例函数y=-$\frac{6}{x}$第四象限的图象上,
∴S△DFO=$\frac{1}{2}$×|-6|=3.
∵S△BAF=4S△DFO,
∴4+$\frac{12}{n}$=4×3,
解得:n=$\frac{3}{2}$,
经验证,n=$\frac{3}{2}$是分式方程4+$\frac{12}{n}$=4×3的解,
∴点D的坐标为($\frac{3}{2}$,-4).
点评 本题考查了解直角三角形、反比例函数图象上点的坐标特征、三角形的面积公式以及反比例函数系数k的几何意义,解题的关键是:(1)求出点C的坐标;(2)根据三角形的面积间的关系找出关于n的分式方程.本题属于中档题,难度不大,但较繁琐,解决该题型题目时,找出点的坐标,再利用反比例函数图象上点的坐标特征求出反比例函数系数是关键.

| A. | 在2到3之间 | B. | 在3到4之间 | C. | 在4到5之间 | D. | 在5到6之间 |
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
| A. | $\frac{2}{3}$ | B. | 1 | C. | -3 | D. | 0 |
| A. | 4x2y2 | B. | 4xy2 | C. | 2x2y2 | D. | 4x2y |
| A. | -4 | B. | 2 | C. | 5 | D. | 8 |
| A. | (x-1)2=x2-1 | B. | -(-2ab2)2=-4a2b4 | C. | (-$\frac{1}{2}$)-2=1 | D. | (-x+1)(-x-1)=-x2-1 |
 如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )
如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )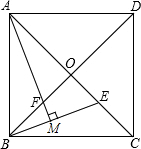 如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.