题目内容
4. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
分析 连接CD,可得出∠OBD=∠OCD,根据点D(0,3),C(4,0),得OD=3,OC=4,由勾股定理得出CD=5,再在直角三角形中得出利用三角函数求出sin∠OBD即可.
解答  解:∵D(0,3),C(4,0),
解:∵D(0,3),C(4,0),
∴OD=3,OC=4,
∵∠COD=90°,
∴CD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
连接CD,如图所示:
∵∠OBD=∠OCD,
∴sin∠OBD=sin∠OCD=$\frac{OD}{CD}$=$\frac{3}{5}$.
故选:D.
点评 本题考查了圆周角定理,勾股定理、以及锐角三角函数的定义;熟练掌握圆周角定理是解决问题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
14.在数-2,1,0,2中,其中最小的是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
15.下列各式运算正确的是( )
| A. | (x-1)2=x2-1 | B. | -(-2ab2)2=-4a2b4 | C. | (-$\frac{1}{2}$)-2=1 | D. | (-x+1)(-x-1)=-x2-1 |
9.下列图形既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列代数运算正确的是( )
| A. | x•x6=x6 | B. | (x2)3=x6 | C. | (x+2)2=x2+4 | D. | (2x)3=2x3 |
14. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )| A. | △AFD≌△DCE | B. | AF=$\frac{1}{2}$AD | C. | AB=AF | D. | BE=AD-DF |
 如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )
如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )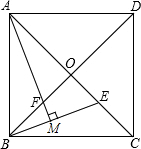 如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.