题目内容
2.点(2,-4)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点在此函数图象上的是( )| A. | (2,4) | B. | (-1,-8) | C. | (-2,-4) | D. | (4,-2) |
分析 由点(2,-4)在反比例函数图象上结合反比例函数图象上点的坐标特征,即可求出k值,再去验证四个选项中横纵坐标之积是否为k值,由此即可得出结论.
解答 解:∵点(2,-4)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=2×(-4)=-8.
∵A中2×4=8;B中-1×(-8)=8;C中-2×(-4)=8;D中4×(-2)=-8,
∴点(4,-2)在反比例函数y=$\frac{k}{x}$的图象上.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征,解题的关键是求出反比例系数k.本题属于基础题,难度不大,解决该题型题目时,结合点的坐标利用反比例函数图象上点的坐标特征求出k值是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
17.下列计算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | (-3)2=6 | C. | 3a4-2a2=a2 | D. | (-a3)2=a5 |
7.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签确定一个小组进行展示活动,则第3个小组被抽到的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{21}$ | D. | $\frac{1}{10}$ |
14. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )| A. | △AFD≌△DCE | B. | AF=$\frac{1}{2}$AD | C. | AB=AF | D. | BE=AD-DF |
 如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )
如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )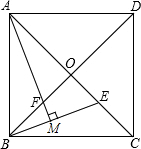 如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.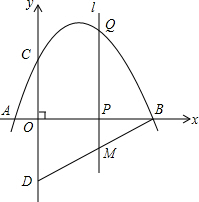 如图,抛物线y=-$\frac{1}{2}{x}^{2}+\frac{3}{2}x+2$与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=-$\frac{1}{2}{x}^{2}+\frac{3}{2}x+2$与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.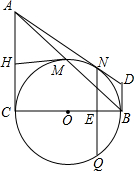 如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.
如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为4πcm2.
如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为4πcm2.