题目内容
4.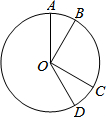 如图,⊙O的半径为3,点A,B,C,D都在⊙O上,∠AOB=30°,将扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,则$\widehat{AD}$的长为$\frac{5}{2}$π.(结果保留π)
如图,⊙O的半径为3,点A,B,C,D都在⊙O上,∠AOB=30°,将扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,则$\widehat{AD}$的长为$\frac{5}{2}$π.(结果保留π)
分析 先利用旋转的性质得到∠BOD=120°,则∠AOD=150°,然后根据弧长公式计算$\widehat{AD}$的长.
解答 解:∵扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,
∴∠BOD=120°,
∴∠AOD=∠AOB+∠BOD=30°+120°=150°,
∴$\widehat{AD}$的长=$\frac{150•π•3}{180}$=$\frac{5}{2}$π.
故答案为$\frac{5}{2}$π.
点评 本题考查了弧长的计算:记住弧长公式l=$\frac{n•π•R}{180}$(弧长为l,圆心角度数为n,圆的半径为R).也考查了旋转的性质.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100m,则池底的最大面积是( )
| A. | 600 m2 | B. | 625 m2 | C. | 650 m2 | D. | 675 m2 |
15.图中各图是按照一定规律排列的羊的组图,图①有1只羊,图②有3只羊,…,则图⑩有( )只羊.


| A. | 53 | B. | 54 | C. | 55 | D. | 56 |
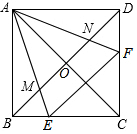 如图,点E,F分别为正方形ABCD的边BC,CD上一点,AC,BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△AEF=2S△AMN
如图,点E,F分别为正方形ABCD的边BC,CD上一点,AC,BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△AEF=2S△AMN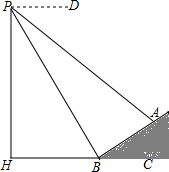 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为200米.
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为200米.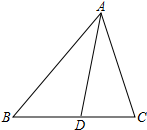 如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$.
如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$.