题目内容
6．解不等式（组）（1）3x+5＜6（x-2）
（2）$\left\{\begin{array}{l}{\frac{x-3}{4}+6≤\frac{1}{2}x①}\\{4-5（x-2）＞8-2x②}\end{array}\right.$．
分析 （1）去括号，移项，合并同类项，系数化成1即可．
（2）根据不等式的性质求出不等式的解集，根据找不等式组解集的规律找出即可．
解答 解：（1）3x+5＜6（x-2），
3x+5＜6x-12，
3x-6x＜-12-5，
-3x＜-17
x＞$\frac{17}{3}$；
（2）$\left\{\begin{array}{l}{\frac{x-3}{4}+6≤\frac{1}{2}x①}\\{4-5（x-2）＞8-2x②}\end{array}\right.$
由①得：x≥21，
由②得：x＜2，
所以不等式组无解．
点评 本题主要考查对解一元一次不等式组，解一元一次不等式，不等式的性质，能求出不等式组的解集是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
17．
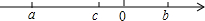已知，三个实数a，b，c在数轴上的点如图所示，|a-b|+|c-a|-|c+b|的值可能是（ ）
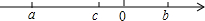已知，三个实数a，b，c在数轴上的点如图所示，|a-b|+|c-a|-|c+b|的值可能是（ ）| A． | 2a | B． | 2b | C． | 2c | D． | -2a |
14．下列各式中最简二次根式为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{{x}^{2}}$ | C． | $\sqrt{0.7}$ | D． | $\sqrt{\frac{1}{3}}$ |
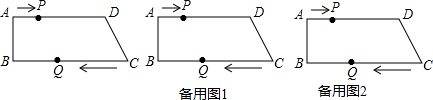
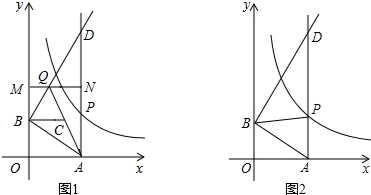
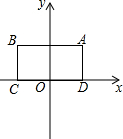对于⊙P及一个矩形给出如下定义：如果⊙P上存在到此矩形四个顶点距离都相等的点，那么称⊙P是该矩形的“等距圆”．如图，在平面直角坐标系xOy中，矩形ABCD的顶点A的坐标为（$\sqrt{3}$，2），顶点C、D在x轴上，且OC=OD．
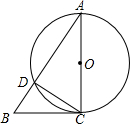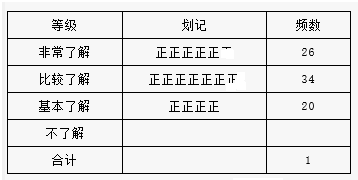
如图，AC是⊙O的直径，∠A=30°，AB交⊙O于D，CD=1，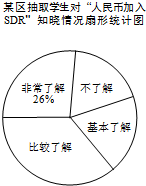
“世界那么大，我想去看看”一句话红遍网络，随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR（特别提款权），以后出国看世界更加方便．为了解某区6000名初中生对“人民币加入SDR”知晓的情况，某校数学兴趣小组随机抽取区内部分初中生进行问卷调查，将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级，并将调查结果整理分析，得到下列图表：