题目内容
12. 己知常数a(a是常数)满足下面两个条件:
己知常数a(a是常数)满足下面两个条件:①二次函数y1=-$\frac{1}{3}$(x+4)(x-5a-7)的图象与x轴的两个交点于坐标原点的两侧;
②一次函数y2=ax+2的图象在一、二、四象限;
(1)求整数a的值;
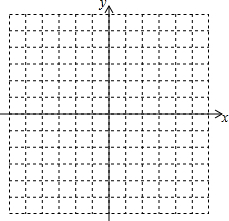
(2)在所给直角坐标系中分别画出y1、y2的图象,并求当y1<y2时,自变量x的取值范围.
分析 (1)利用抛物线与x轴的交点问题得到抛物线与x轴的两个交点坐标为(-4,0),(5a+7,0),利用抛物线与x轴的两个交点与坐标原点的两侧得到5a+7>0,则a>-$\frac{7}{5}$,再利用一次函数性质得到a<0,于是得到a的范围为-$\frac{7}{5}$<a<0,然后在此范围内找出整数即可;
(2)由(1)得抛物线解析式为y1=-$\frac{1}{3}$(x+4)(x-2)=-$\frac{1}{3}$(x+1)2+3,直线解析式为y=-x+2,再利用描点法画出两函数图象,然后找出一次函数图象在抛物线上方所对应的x的范围即可.
解答 解:(1)抛物线y1=-$\frac{1}{3}$(x+4)(x-5a-7)的图象与x轴的两个交点坐标为(-4,0),(5a+7,0),
根据题意得5a+7>0,解得a>-$\frac{7}{5}$,
又因为一次函数y2=ax+2的图象在一、二、四象限,则a<0,
所以a的范围为-$\frac{7}{5}$<a<0,
所以整数a为-1;
(2)抛物线解析式为y1=-$\frac{1}{3}$(x+4)(x-2)=-$\frac{1}{3}$(x+1)2+3,抛物线的顶点坐标为(-1,3),
直线解析式为y=-x+2,
如图,
当x<-1或x>2时,y1<y2.
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了一次函数的性质和观察函数图象的能力.

练习册系列答案
相关题目
2. 如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )
如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )
 如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )
如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )| A. | 25° | B. | 30° | C. | 40° | D. | 55° |
20.圆锥的侧面展开图是( )
| A. | 扇形 | B. | 等腰三角形 | C. | 圆 | D. | 矩形 |
7.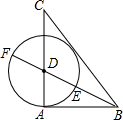 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
17. 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
2.如图,图①由4个正三角形和3个正六边形拼成,图②由8个正三角形和5个正六边形拼成,图③由12个正三角形和7个正六边形拼成,依次规律,则第n个图案中,正三角形和正六边形的个数分别是( )


| A. | n2+n+2,2n+1 | B. | 2n+2,2n+1 | C. | 4n,n2-n+3 | D. | 4n,2n+1 |
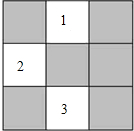 某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.
某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.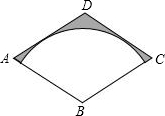 如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π.
如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π.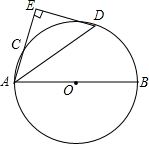 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.