题目内容
16.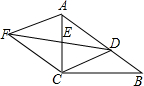 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF.(1)求证:四边形ADCF是平行四边形;
(2)当点D是AB的中点时,若AB=4,求四边形ADCF的周长.
分析 (1)根据两组对边分别平行的四边形是平行四边形即可判定.
(2)只要证明四边形ADCF是菱形即可解决问题.
解答 (1)证明:∵点E是AC的中点,
∴AE=EC,
∵EF=DE,
∴四边形ADCF是平行四边形.
(2)解:∵∠ACB=90°,点DAB的中点,
∴CD=AD=$\frac{1}{2}$AB=2,
∴平行四边形ADCF是菱形,
∴菱形ADC的周长8.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质等知识,熟练记住平行四边形、菱形的判定和性质是解题的关键,属于参考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.在平面直角坐标系中,点M(-2,6)关于原点对称的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.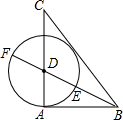 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.已知⊙O1与⊙O2外离,⊙O1的半径是5,圆心距O1O2=7,那么⊙O2的半径可以是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
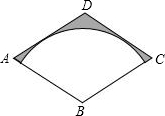 如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π.
如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π. 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;过点B的直线DE分别交l1、l3于点D、E.若AB=2,BC=4,BD=1.5,则线段BE的长为3.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;过点B的直线DE分别交l1、l3于点D、E.若AB=2,BC=4,BD=1.5,则线段BE的长为3.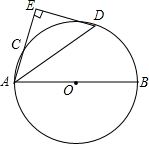 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.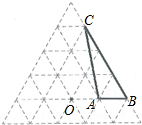 如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.
如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.