题目内容
15. 如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且
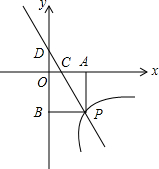
如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且OA=OB,$\frac{OC}{CA}$=$\frac{1}{2}$,则m=-4,$\frac{{S}_{△APC}}{{S}_{△DPB}}$=$\frac{2}{3}$.
分析 由一次函数y=kx+1的图象交y轴于点D,得出点D的坐标为(0,1);设OC=a,根据$\frac{OC}{CA}$=$\frac{1}{2}$得到CA=2OC=2a,那么OA=3a=OB,P(3a,-3a).根据△DOC∽△DBP,利用相似三角形对应边成比例得出$\frac{1}{1+3a}$=$\frac{a}{3a}$=$\frac{1}{3}$,求出a=$\frac{2}{3}$,那么P(2,-2),再根据待定系数法求出m=2×(-2)=-4;根据相似三角形面积之比等于相似比的平方得出$\frac{{S}_{△APC}}{{S}_{△DPB}}$=($\frac{AP}{DB}$)2=$\frac{4}{9}$.
解答 解:∵一次函数y=kx+1的图象交y轴于点D,
令x=0,得y=1,
∴点D的坐标为(0,1);
设OC=a,则CA=2OC=2a,OA=3a=OB,P(3a,-3a).
∵OC∥BP,
∴△DOC∽△DBP,
∴$\frac{DO}{DB}$=$\frac{OC}{BP}$,即$\frac{1}{1+3a}$=$\frac{a}{3a}$=$\frac{1}{3}$,
∴a=$\frac{2}{3}$,
∴P(2,-2).
∵反比例函数y=$\frac{m}{x}$(x>0)的图象过点P,
∴m=2×(-2)=-4;
$\frac{{S}_{△APC}}{{S}_{△DPB}}$=($\frac{AP}{DB}$)2=($\frac{2}{3}$)2=$\frac{4}{9}$.
故答案为-4;$\frac{4}{9}$.
点评 本题考查了反比例函数与一次函数的交点问题,反比例函数解析式的确定,相似三角形的判定与性质,图形的面积求法等知识,求出点P的坐标是解题的关键.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 14 | B. | 20 | C. | 28 | D. | 40 |
| A. | 扇形 | B. | 等腰三角形 | C. | 圆 | D. | 矩形 |
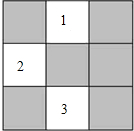 某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.
某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.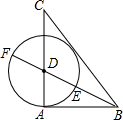 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论: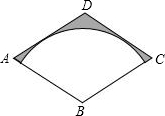 如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π.
如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π.