题目内容
17.求值:(2a-1)2+(a-2)(a+2)-4a(a-$\frac{1}{2}$),其中a=-1.分析 运用完全平方公式、平方差公式及单项式乘多项式法则进行运算,再合并同类项即可化简,最后将a=-1代入可得.
解答 解:原式=4a2-4a+1+a2-4-4a2+2a
=a2-2a-3,
当a=-1时,
原式=(-1)2-2×(-1)-3
=1+2-3
=0.
点评 本题主要考查整式的运算化简能力,熟练掌握公式及整式的运算法则是解题的根本和关键.

练习册系列答案
相关题目
7.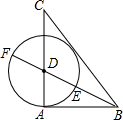 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.已知⊙O1与⊙O2外离,⊙O1的半径是5,圆心距O1O2=7,那么⊙O2的半径可以是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
2.如图,图①由4个正三角形和3个正六边形拼成,图②由8个正三角形和5个正六边形拼成,图③由12个正三角形和7个正六边形拼成,依次规律,则第n个图案中,正三角形和正六边形的个数分别是( )


| A. | n2+n+2,2n+1 | B. | 2n+2,2n+1 | C. | 4n,n2-n+3 | D. | 4n,2n+1 |
9. 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表:
(1)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人.
(2)求训练后篮球定点投篮人均进球数为多少个?
(3)根据测试资料,参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.训练后篮球定点投篮测试进球统计表:
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(2)求训练后篮球定点投篮人均进球数为多少个?
(3)根据测试资料,参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
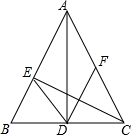 如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.
如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.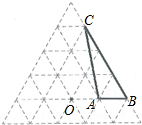 如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.
如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.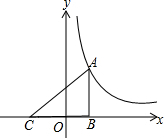 如图,点A是反比例函数y=$\frac{k}{x}$(x>0)图象上一点,AB⊥x轴于点B,点C在x轴上,且OB=OC,若△ABC的面积等于6,则k的值等于( )
如图,点A是反比例函数y=$\frac{k}{x}$(x>0)图象上一点,AB⊥x轴于点B,点C在x轴上,且OB=OC,若△ABC的面积等于6,则k的值等于( )