题目内容
18. 如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点
如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点P(2016,a),则a=24.
分析 先通过解方程x2-10x=0得到A1(10,0),则OA1=10,利用旋转的性质得A1A2=A2A3=10,由于2010=10×201,则可判断P(2016,a)在抛物线C202上,由于抛物线C202的开口向下,与x轴的两交点坐标为(2010,2020),则可求出抛物线C202的解析式为y=-(x-2010)(x-2020),然后把P(2016,a)代入可计算出a的值.
解答 解:当y=0时,x2-10x=0,解得x1=10,x2=0,则A1(10,0)
所以OA1=10,
所以A1A2=A2A3=10,
而2010=10×201,
∴P(2016,a)在抛物线C202上,抛物线C202的开口向下,与x轴的两交点坐标为(2010,2020),
所以抛物线C202的解析式为y=-(x-2010)(x-2020),
当x=2016时,y=-(2016-2010)(2016-2020)=24,即a=24.
故答案为24.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
8.二次根式$\frac{1}{{\sqrt{x+1}}}$在实数范围有意义,则x的取值范围是( )
| A. | x≥-1 | B. | x≠-1 | C. | x>-1 | D. | x≤-1 |
9.谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石,某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.6 |
| B | 10 | 50 | 0.8 |
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
6.在平面直角坐标系中,点M(-2,6)关于原点对称的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.若菱形的两条对角线的长分别为6,8.则此菱形的周长是( )
| A. | 14 | B. | 20 | C. | 28 | D. | 40 |
7.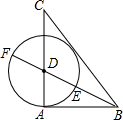 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.已知⊙O1与⊙O2外离,⊙O1的半径是5,圆心距O1O2=7,那么⊙O2的半径可以是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
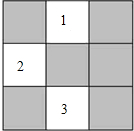 某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.
某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.