题目内容
8. 甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)
甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)
分析 如图,作FG⊥AB于G,DH⊥AB于H.设AG=x.在Rt△AFG中,用x表示FG,在Rt△ADH中,用x表示DH,根据FG-DH=EB-BC=EC,列出方程即可解决问题.
解答 解:如图,作FG⊥AB于G,DH⊥AB于H.设AG=x.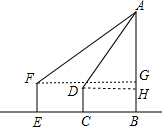
在Rt△AFG中,FG=$\frac{AG}{tan50°}$=$\frac{x}{\frac{19}{20}}$=$\frac{20x}{19}$,
在Rt△ADH中,DH=$\frac{AH}{tan72°}$=$\frac{6(x+0.3)}{19}$,
∵FG-DH=EB-CB=EC,
∴$\frac{20x}{19}$-$\frac{6(x+0.3)}{19}$=10,
解得x=13.7,
∴AB=AG+BG=AG+EF=13.7+1.8=15.5米,
答:灯塔AB的高度为15.5米.
点评 本题考查解直角三角形,矩形的性质.锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.

练习册系列答案
相关题目
5. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )| A. | ∠1=∠3 | B. | ∠2+∠4=180° | C. | ∠1=∠4 | D. | ∠3=∠4 |
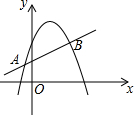 如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.
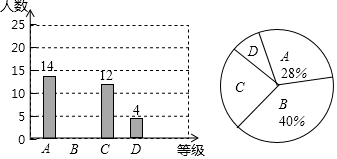
如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.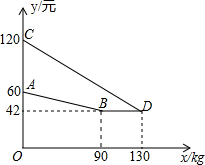 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.