题目内容
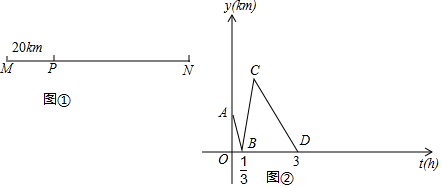
17.如图①,在一条笔直的公路上有M、P、N三个地点,M、P两地相距20km,甲开汽车,乙骑自行车分别从M、P两地同时出发,匀速前往N地,到达N地后停止运动.已知乙骑自行车的速度为20km/h,甲,乙两人之间的距离y(km)与乙行驶的时间t(h)之间的关系如图②所示.(1)M、N两地之间的距离为80km;
(2)求线段BC所表示的y与t之间的函数表达式;
(3)若乙到达N地后,甲,乙立即以各自原速度返回M地,请在图②所给的直角坐标系中补全函数图象.
分析 (1)根据路程=速度×时间,可求PM,再计算20即可求解;
(2)由题意可知B($\frac{1}{3}$,0),C(1,40),根据待定系数法可求线段BC所表示的y与t之间的函数表达式;
(3)当甲开汽车返回M地时,甲,乙两人之间的距离y(km)最大为60;依此补全函数图象.
解答 解:(1)20×3+20
=60+20
=80(km).
答:M、N两地之间的距离为80km;
(2)由题意可知B($\frac{1}{3}$,0),C(1,40),
设y与x之间的函数表达式为y=kx+b.
根据题意得,
当x=$\frac{1}{3}$时,y=0;
当x=1时,y=40.
所以$\left\{\begin{array}{l}\frac{1}{3}k+b=2\\ k+b=40\end{array}$,
解得$\left\{\begin{array}{l}k=60\\ b=-20\end{array}$.
所以,y与x之间的函数表达式为y=60x-20;
(3)如图所示:
故答案为:80.
点评 此题主要考查了一次函数的应用,利用图表中数据得出汽车速度是解题关键.

练习册系列答案
相关题目
12.由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
| 售价(元/台) | 月销售量(台) |
| 400 | 200 |
| 390 | 250 |
| x | -5x+2200 |
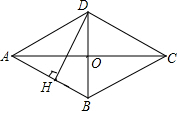 如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为$\frac{50}{13}$.
如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为$\frac{50}{13}$. 甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)
甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)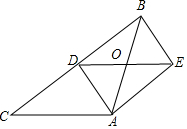 如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.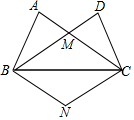 如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.
如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.