题目内容
18．某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．（1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y（件）和销售该品牌玩具获得利润w（元）；
（2）求该玩具销售单价x为多少元时，商场获得最大利润，并求出最大利润．
分析 （1）根据“实际销量=原销量-降低的价格×每降1元少售出的件数”可得销量y的函数解析式，根据“总利润=每件利润×降价后的销售量”可得w的函数解析式；
（2）将（1）中函数解析式配方成顶点式即可得出函数的最大值．
解答 解：（1）根据题意，得：y=600-10（x-40），
w=（x-30）[600-10（x-40）]；
（2）w=-10x2+1300x-30000=-10（x-65）2+12250，
∴当x=65时，w最大=12250，
答：当该玩具销售单价为65元时，商场获得最大利润12250元．
点评 本题主要考查二次函数的应用，根据题意确定实际销量y关于销售单价的解析式，由总利润的相等关系列出总利润的函数解析式是解题的关键．
练习册系列答案
相关题目
甲、乙两人要测量灯塔AB的高度，甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°，乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°，点B、C、E在同一条直线上，且甲乙两人的距离CE=10米，请你根据所测量的数据计算灯塔AB的高度．（结果精确到0.1m）（参考数据：sin50°≈$\frac{4}{5}$，cos50°≈$\frac{16}{25}$，tan50°≈$\frac{5}{4}$，sin72°≈$\frac{19}{20}$，cos72°≈$\frac{3}{10}$，tan72°≈$\frac{19}{6}$）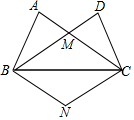
如图，在△ABC和△BCD中，AB=DC，AC=DB，AC、DB交于点M．
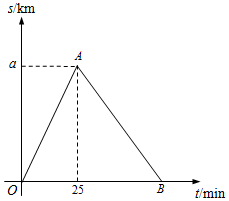某市举行“迷你马拉松”长跑比赛，运动员从起点甲地出发，跑到乙地后，沿原路线再跑回点甲地．设该运动员离开起点甲地的路程s（km）与跑步时间t（min）之间的函数关系如图所示．已知该运动员从甲地跑到乙地时的平均速度是0.2km/min，根据图象提供的信息，解答下列问题：