题目内容
13.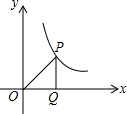 如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )
如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )| A. | $s=\frac{k}{4}$ | B. | $s=\frac{k}{2}$ | C. | s=k | D. | 不能确定 |
分析 根据点P在反比例函数图象上结合反比例函数系数k的几何意义就可以求出s与k之间的数量关系.
解答 解:∵点P是反比例函数y=$\frac{k}{x}$图象上一点,且PQ⊥x轴于点Q,
∴S△POQ=$\frac{1}{2}$|k|=s,
解得:|k|=2s.
∵反比例函数在第一象限有图象,
∴k=2s.即s=$\frac{k}{2}$
故选:B.
点评 本题考查了反比例函数的性质以及反比例函数系数k的几何意义,解题的关键是根据反比例函数系数k的几何意义找出△POQ面积s与k的关系.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
3.一个正多边形每一个外角为36°,则这个多边形的内角和为( )
| A. | 360° | B. | 1440° | C. | 1800° | D. | 2160° |
1.已知点(-4,y1),(2,y2)都在直线y=-2x+3上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
5.已知xy>0,化简二次根式$x\sqrt{-\frac{y}{x^2}}$的正确结果是( )
| A. | $-\sqrt{-y}$ | B. | $-\sqrt{y}$ | C. | $\sqrt{-y}$ | D. | $\sqrt{y}$ |
 如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=58°.
如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=58°.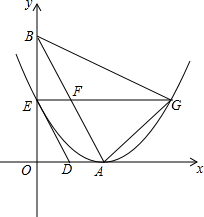 如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F. 如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是24.
如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是24.