题目内容
18．如果反比例函数y=$\frac{k}{x}$（k≠0）的图象在每个象限内，y随着x的增大而减小，那么请你写出一个满足条件的反比例函数解析式y=$\frac{1}{x}$（答案不唯一）（只需写一个）．分析 先根据函数的增减性判断出k的符号，进而可得出结论．
解答 解：∵反比例函数y=$\frac{k}{x}$（k≠0）的图象在每个象限内，y随着x的增大而减小，
∴k＞0，
∴满足条件的反比例函数解析式可以是y=$\frac{1}{x}$．
故答案为：y=$\frac{1}{x}$（答案不唯一）．
点评 本题考查的是反比例函数的性质，熟知反比例函数的增减性是解答此题的关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
9．若分式$\frac{x}{x-3}$有意义，则x满足的条件是（ ）
| A． | x≠0 | B． | x≠3 | C． | x≠-3 | D． | x≠±3 |
13．
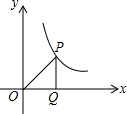如图，点P在反比例函数y=$\frac{k}{x}$（x＞0）第一象限的图象上，PQ垂直x轴，垂足为Q，设△POQ的面积是s，那么s与k之间的数量关系是（ ）
如图，点P在反比例函数y=$\frac{k}{x}$（x＞0）第一象限的图象上，PQ垂直x轴，垂足为Q，设△POQ的面积是s，那么s与k之间的数量关系是（ ）| A． | $s=\frac{k}{4}$ | B． | $s=\frac{k}{2}$ | C． | s=k | D． | 不能确定 |
3．用配方法解方程x2-2x-99=0时，原方程变形为（ ）
| A． | （x+1）2=100 | B． | （x-1）2=100 | C． | （x+1）2=98 | D． | （x-1）2=98 |
7．已知点（a-1，y1）、（a+1，y2）在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，若y1＜y2，则a的范围是（ ）
| A． | a＞1 | B． | a＜-1 | C． | -1＜a＜1 | D． | -1＜a＜0或0＜a＜1 |
如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB