题目内容
5.已知xy>0,化简二次根式$x\sqrt{-\frac{y}{x^2}}$的正确结果是( )| A. | $-\sqrt{-y}$ | B. | $-\sqrt{y}$ | C. | $\sqrt{-y}$ | D. | $\sqrt{y}$ |
分析 二次根式有意义,y<0,结合已知条件得y<0,化简即可得出最简形式.
解答 解:根据题意,xy>0,
得x和y同号,
又∵$x\sqrt{-\frac{y}{x^2}}$中-$\frac{y}{{x}^{2}}$≥0,
∴y<0,
∴x<0,y<0,
则原式=x•$\frac{\sqrt{-y}}{\sqrt{{x}^{2}}}$=x•$\frac{\sqrt{-y}}{-x}$=-$\sqrt{-y}$,
故选:A.
点评 主要考查了二次根式的化简,注意开平方的结果为非负数是解题的关键.

练习册系列答案
相关题目
13.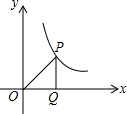 如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )
如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )
 如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )
如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )| A. | $s=\frac{k}{4}$ | B. | $s=\frac{k}{2}$ | C. | s=k | D. | 不能确定 |
14.点A(-3,-2)向上平移2个单位,再向右平移2个单位到点B,则点B的坐标为( )
| A. | (1,0) | B. | (1,-4) | C. | (-1,0) | D. | (-5,-1) |
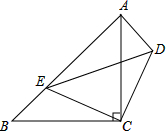 如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.
如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.