题目内容
13.在△ABC中,∠ACB=90°,BC=1,AC=2,则下列正确的是( )| A. | sinA=$\frac{2\sqrt{5}}{5}$ | B. | tanA=$\frac{\sqrt{5}}{5}$ | C. | cosB=$\frac{\sqrt{5}}{5}$ | D. | tanB=$\frac{1}{2}$ |
分析 先根据勾股定理得出AB,再根据三角函数的定义分别得出sinA,tanA,cosB,tanB即可.
解答 解:∵∠ACB=90°,BC=1,AC=2,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴sinA=$\frac{BC}{AB}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
tanA=$\frac{BC}{AC}$=$\frac{1}{2}$,
cosB=$\frac{BC}{AB}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
tanB=$\frac{AC}{BC}$=2,
故选C.
点评 本题考查了锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
3.下列从左到右变形正确的是( )
| A. | $\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$ | B. | $\frac{{x-\frac{1}{2}y}}{{\frac{1}{2}x+y}}=\frac{2x-y}{x+2y}$ | ||
| C. | $-\frac{x+1}{x-y}=\frac{x-1}{x-y}$ | D. | $\frac{a+b}{a-b}=\frac{a-b}{a+b}$ |
4.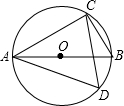 如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )
如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )
 如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )
如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
1.如果a>b,下列各式中不正确的是( )
| A. | a-4>b-4 | B. | -2a<-2b | C. | -5+a<-5+b | D. | -$\frac{a}{3}$<-$\frac{b}{3}$ |
8.化简(x+1)-(1-x)+(x-1)的结果是( )
| A. | x-1 | B. | 3x+1 | C. | 3x-3 | D. | 3x-1 |
5.化简(1-$\frac{2}{x+1}$)÷$\frac{1}{{x}^{2}-1}$的结果是( )
| A. | (x+1)2 | B. | (x-1)2 | C. | $\frac{1}{(x+1)^{2}}$ | D. | $\frac{1}{(x-1)^{2}}$ |
2.给你一副三角板画角,不可能画出的角是( )
| A. | 15° | B. | 135° | C. | 165° | D. | 100° |
 如图,四边形ABCD,CDMF,MFEG都是正方形,BD,AE相交于点H,求tan∠AHB.
如图,四边形ABCD,CDMF,MFEG都是正方形,BD,AE相交于点H,求tan∠AHB.