题目内容
7. 如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.
如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.(1)求抛物线的函数关系式;
(2)当△DQM的面积等于△PQM面积时,求m的值;
(3)请求出PD+QD的最大值.
分析 (1)根据对称轴公式x=-$\frac{b}{2a}$即可解决问题.
(2)利用方程组求出点D坐标,再求出点Q坐标,根据中点坐标公式,可得点P坐标,利用待定系数法即可解决问题.
(3)如图,作CG⊥y轴于G,PD的延长线交GC于E,作PF⊥CG于F.因为直线PD的解析式为y=x+m,直线BC的解析式为y=-x+6,可知BC⊥PE,△CQE,△CDQ,△CDE,△PFE都是等腰直角三角形,推出DQ=CD=DE,所以DQ+DP=DE+DP=PE,所以欲求DQ+DP的最大值,只要求PE的最大值,因为当PF最大时,PE最大,所以当点P与点M重合时,PF最大,由此即可解决问题.
解答 解:(1)由题意抛物线的对称轴x=2,
∴-$\frac{-1}{2a}$=2,
∴a=$\frac{1}{4}$,
∴抛物线的解析式为y=$\frac{1}{4}$x2-x-3.
(2)对于抛物线y=$\frac{1}{4}$x2-x-3,令y=0,得$\frac{1}{4}$x2-x-3=0,解得x=-2或6,
∴A(-2,0),B(6,0),
∵C(2,4),
∴直线BC的解析式为y=-x+6,
由$\left\{\begin{array}{l}{y=-x+6}\\{y=x+m}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{6-m}{2}}\\{y=\frac{m+6}{2}}\end{array}\right.$,
∴D($\frac{6-m}{2}$,$\frac{m+6}{2}$),
∵Q(2,2+m),
∵△DQM的面积等于△PQM面积,
∴PQ=DQ,
∴P($\frac{2+m}{2}$,$\frac{2+3m}{2}$),
把P($\frac{2+m}{2}$,$\frac{2+3m}{2}$)代入y=$\frac{1}{4}$x2-x-3得$\frac{2+3m}{2}$=$\frac{1}{4}$($\frac{2+m}{2}$)2-$\frac{2+m}{2}$-3,
整理得m2-28m-76=0,
解得m=14-4$\sqrt{17}$或14+4$\sqrt{17}$(舍弃),
(3)如图,作CG⊥y轴于G,PD的延长线交GC于E,作PF⊥CG于F.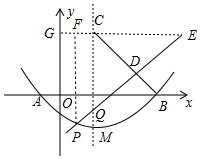
∵直线PD的解析式为y=x+m,直线BC的解析式为y=-x+6,
∴BC⊥PE,△CQE,△CDQ,△CDE,△PFE都是等腰直角三角形,
∴DQ=CD=DE,
∴DQ+DP=DE+DP=PE,
∴欲求DQ+DP的最大值,只要求PE的最大值,
∵当PF最大时,PE最大,
∴当点P与点M重合时,PF最大,
∵C(2,4),M(2,-4),
∴PF的最大值为8,
∴PE的最大值为8$\sqrt{2}$,
∴DQ+DP的最大值为8$\sqrt{2}$.
点评 本题考查二次函数综合题、一次函数的应用、待定系数法、等腰直角三角形的判定和性质、中点坐标公式等知识,解题的关键是灵活运用待定系数法解决问题,学会用转化的思想思考问题,本题的突破点是把求DQ+DP的最大值转化为求等腰直角三角形△EFP的斜边的最大值,属于中考压轴题.

 阶梯计算系列答案
阶梯计算系列答案| A. | 5 | B. | 4 | C. | 3 | D. | $\sqrt{5}$ |
 如图,图形的对称轴的条数是( )
如图,图形的对称轴的条数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
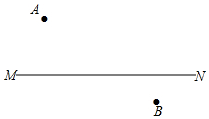 如图,在直线MN的异侧有A、B两点,按要求画图取点,并写出画图的依据.
如图,在直线MN的异侧有A、B两点,按要求画图取点,并写出画图的依据.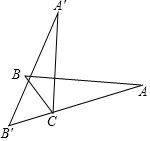 如图,在△ABC中,∠A:∠B:∠ACB=2:5:11,若将△ACB绕点C逆时针旋转,使旋转前后的△A′B′C中的顶点B′在原三角形的边AC的延长线上,求∠BCA′的度数.
如图,在△ABC中,∠A:∠B:∠ACB=2:5:11,若将△ACB绕点C逆时针旋转,使旋转前后的△A′B′C中的顶点B′在原三角形的边AC的延长线上,求∠BCA′的度数. 如图,小龙在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小龙的前后身高相同(即PE=QF),两个路灯的高度相同(即AC=BD)
如图,小龙在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小龙的前后身高相同(即PE=QF),两个路灯的高度相同(即AC=BD)