题目内容
18.已知等腰三角形的底边长为2,则该三角形的周长可以是( )| A. | 5 | B. | 4 | C. | 3 | D. | $\sqrt{5}$ |
分析 根据三角形三边关系,利用代入法,对各个选项进行分析,从而不能求解.
解答 解:A,当周长为5,底边为2时,腰长和为3,因为3>2,故能构成三角形;
B,当周长为4,底边长为2时,腰长和为2,因为2=2,故不能构成三角形;
C,当周长为3,底边为2时,腰长和为1,因为1<2,故不能构成三角形;
D,当周长为$\sqrt{5}$≈2.236,底边为2时,腰长和为0.236,因为0.236<2,故不能构成三角形;
故选A.
点评 此题主要考查等腰三角形的性质及三角形三边关系的综合运用,关键是熟悉三角形三边关系定理:三角形两边之和大于第三边.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
10.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.(-x2+3xy-0.5y2)-(-0.5x2+4xy-1.5y2)=-0.5x2 +y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
 +y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )| A. | -7xy | B. | -xy | C. | 7xy | D. | xy |
9.一个多边形截去一个角后,形成一个六边形,那么原多边形边数为( )
| A. | 5 | B. | 5或6 | C. | 5或7 | D. | 5或6或7 |
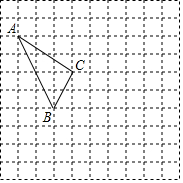 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3). 如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.
如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.