题目内容
12. 如图,小龙在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小龙的前后身高相同(即PE=QF),两个路灯的高度相同(即AC=BD)
如图,小龙在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小龙的前后身高相同(即PE=QF),两个路灯的高度相同(即AC=BD)(1)求证:AP=BQ;
(2)若FQ=1.6m,AC=9.6m,求两个路灯之间的距离.
分析 (1)先证明△APE∽△ABD,利用相似比可得AP=$\frac{1}{6}$AB,再证明△BQF∽△BAC,利用相似比可得BQ=$\frac{1}{6}$AB,从而证得AP=BQ;
(2)则$\frac{1}{6}$AB+12+$\frac{1}{6}$AB=AB,解得AB=18(m);
解答 解:(1)∵PE∥BD,
∴△APE∽△ABD,
∴$\frac{AP}{AB}$=$\frac{PE}{BD}$,即$\frac{AP}{AB}$=$\frac{1.6}{9.6}$,
∴AP=$\frac{1}{6}$AB,
∵FQ∥AC,
∴△BQF∽△BAC,
∴$\frac{BQ}{BA}$=$\frac{QF}{AC}$,即$\frac{BQ}{AB}$=$\frac{1.6}{9.6}$,
∴BQ=$\frac{1}{6}$AB,
∴AP=BQ;
(2)∵AP+PQ+BQ=AB,
∴$\frac{1}{6}$AB+12+$\frac{1}{6}$AB=AB,
∴AB=18.
答:两路灯的距离为18m;
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
17.若等式($\sqrt{\frac{x}{3}}$-1)0=1成立,则x的取值范围是( )
| A. | x≠3 | B. | x≥0 | C. | x≥0且x≠3 | D. | x>0且x≠3 |
 如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.
如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.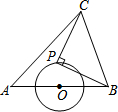 如图,AB=4,O为AB的中点,⊙O的半径为1,点P是⊙O上一动点,以PB为直角边的等腰直角三角形PBC(点P、B、C按逆时针方向排列),则线段AC的长的取值范围为$\sqrt{2}$≤AC≤3$\sqrt{2}$.
如图,AB=4,O为AB的中点,⊙O的半径为1,点P是⊙O上一动点,以PB为直角边的等腰直角三角形PBC(点P、B、C按逆时针方向排列),则线段AC的长的取值范围为$\sqrt{2}$≤AC≤3$\sqrt{2}$.