��Ŀ����
2��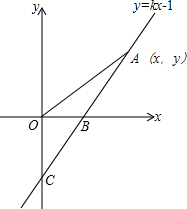 ��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬ֱ��y=kx-1��k��0����x�ᡢy��ֱ���B��C���㣬��OB=$\frac{1}{2}$OC����A��x��y����ֱ��y=kx-1�ϵ�һ�����㣬����OA��
��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬ֱ��y=kx-1��k��0����x�ᡢy��ֱ���B��C���㣬��OB=$\frac{1}{2}$OC����A��x��y����ֱ��y=kx-1�ϵ�һ�����㣬����OA����1����B��������k��ֵ��
��2�����AOB�����S��x֮��ĺ�����ϵʽ��
��3��̽����
�ٵ���A�˶���ʲôλ��ʱ����AOB�������$\frac{1}{4}$��
���ڢٵ������£�y�����Ƿ����һ��P��ʹ��POA�ǵ��������Σ������ڣ���д����������������P������ꣻ�������ڣ���˵�����ɣ�
���� ��1�������OC=1���B�����꣬�����ô���ϵ�������kֵ��
��2�����ðѡ�AOB�������ʾ�������ڸ���S��x֮��Ĺ�ϵ����������
��3�������ã�2���ó�������ϵʽ���ɵó���A�����ꣻ
�ڷ�����������ۼ��㼴�ɣ�
��� �⣺��1��2x2-3x+1=0��
��2x-1����x-1��=0
2x-1=0��x-1=0��
���x1=$\frac{1}{2}$��x2=1��
��OB��OC��
���B��$\frac{1}{2}$��0����
�ѵ�B����y=kx-1�ã�$\frac{1}{2}$k-1=0��
��ã�k=2��
��2��ֱ�߽���ʽΪy=2x-1��
��AOB�����S=$\frac{1}{2}$��$\frac{1}{2}$����2x-1��=$\frac{1}{2}$x-$\frac{1}{4}$��
��3���١�AOB���S=$\frac{1}{2}$x-$\frac{1}{4}$��
��S=$\frac{1}{4}$ʱ��$\frac{1}{2}$x-$\frac{1}{4}$=$\frac{1}{4}$��
��ã�x=1��
��ʱy=1��
���A��������1��1����
�ڴ��������ĵ�P���������£�
�ɢ�֪��A�������ǣ�1��1������OA=$\sqrt{2}$��
��ͼ��
i����O�ǡ�AOP�Ķ��Ƕ���ʱ��OA=OP����P�������ǣ�0��$\sqrt{2}$����0��-$\sqrt{2}$����
ii����A�ǡ�AOP�Ķ��Ƕ���ʱ��AO=AP����P���A����x�ᴹֱ��ֱ�߶Գƣ���P�������ǣ�0��2����
iii����P�ǡ�AOP�Ķ��Ƕ���ʱ��PA=PO������P��0��x������
x=$\sqrt{��x-1��^{2}+1}$��
��ã�x=1��
��P��0��1����
�������������������ĵ�P�������ǣ���0��$\sqrt{2}$����0��-$\sqrt{2}$����0��2����0��1����
���� ������һ�κ����ۺ��⣬��Ҫ�����˽�һԪ���η��̣�����ϵ������һ�κ�������ʽ�������ε�������������������ߺ�һ�����ʣ��ѵ����ڣ�2���ڸ��ݵ��������ε������IJ�ͬ��������ۣ�

 ��У����ϵ�д�
��У����ϵ�д�| A�� | 625��1+x��2=1225 | B�� | 1225��1+x��2=625 | C�� | 625��1-x��2=1225 | D�� | 1225��1-x��2=625 |
| A�� | 0 | B�� | 1 | C�� | -1 | D�� | 2 |
| A�� | $-0.3��-\frac{1}{3}$ | B�� | $-\frac{6}{5}��-\frac{7}{6}$ | C�� | ��-2��3����-2��2 | D�� | $-\frac{9}{10}��-\frac{10}{9}$ |