题目内容
12．
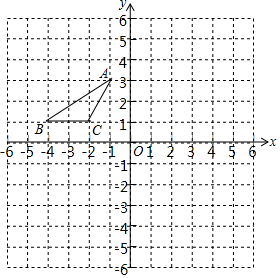如图，方格中，每个小正方形的边长都是单位1，△ABC在平面直角坐标系中的位置如图．（1）画出将△ABC向右平移2个单位得到的△A1B1C1；
（2）画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2；
（3）画出与△ABC关于原点O对称的△A3B3C3，并直接写出点A3的坐标．
分析 （1）直接利用平移的性质得出对应点位置进而得出答案；
（2）直接利用旋转的性质得出对应点位置进而得出答案；
（3）利用关于原点对称点的性质得出对应点位置进而得出答案．
解答 
解：（1）如图所示：△A1B1C1，即为所求；
（2）如图所示：△A2B2C2，即为所求；
（3）如图所示：△A3B3C3，即为所求，点A3的坐标为：（1，-3）．
点评 此题主要考查了平移变换、旋转变换，正确得出对应点位置是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
3．
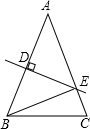已知：如图，在△ABC中，AB=AC，DE是AB的垂直平分线，若BE+CE=12，BC=8，则△ABC的周长为（ ）
已知：如图，在△ABC中，AB=AC，DE是AB的垂直平分线，若BE+CE=12，BC=8，则△ABC的周长为（ ）| A． | 20 | B． | 32 | C． | 24 | D． | 36 |
7．
如图所示，四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH…，如此下去，则第2017个正方形的边长是（ ）
如图所示，四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH…，如此下去，则第2017个正方形的边长是（ ）| A． | ${（{\sqrt{2}}）^{2016}}$ | B． | ${（{\sqrt{2}}）^{2017}}$ | C． | $2016\sqrt{2}$ | D． | $2017\sqrt{2}$ |
17．
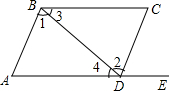如图，给出下列条件：①∠1=∠2；②∠3=∠4；③∠A=∠CDE；④AD∥BC，且∠A=∠C．其中，能推出AB∥DC的条件为（ ）
如图，给出下列条件：①∠1=∠2；②∠3=∠4；③∠A=∠CDE；④AD∥BC，且∠A=∠C．其中，能推出AB∥DC的条件为（ ）| A． | ①④ | B． | ②③ | C． | ①③ | D． | ①③④ |
已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．