题目内容
19. 如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.(1)求证:△DCE∽△BCA;
(2)若AB=3,DE=2.求AC的长.
分析 (1)先证明DE∥AB,然后依据相似三角形的判断定理进行证明即可;
(2)设AC=x,则EC=x-2,然后依据相似三角形的性质列方出求解即可
解答 解:(1)∵在△ABC中,AD是角平分钱,
∴∠BAD=∠EAD.
又∵∠EAD=∠ADE,
∴∠BAD=∠ADE.
∴DE∥AB.
∴△DCE∽△BCA.
(2)∵∠EAD=∠ADE,
∴AE=DE=2.
设AC=x,则EC=x-2.
∵△DCE∽△BCA,
∴$\frac{DE}{AB}$=$\frac{CE}{AC}$.
∴$\frac{2}{3}$=$\frac{x-2}{x}$,解得x=6.
∴AC=6.
点评 本题主要考查的是相似三角形的性质和判定,熟练掌握相似三角形的性质和判定定理是解题的关键.

练习册系列答案
相关题目
9.若a+b=0,则a与b之间的关系是( )
| A. | 相等 | B. | 互为倒数 | ||
| C. | 互为相反数 | D. | 一个是正数一个是负数 |
10.四边形ABCD是正方形,以CD为边向正方形外作正△CDE,则∠EAB的度数为( )
| A. | 75° | B. | 72° | C. | 67.5° | D. | 65° |
7. 如图所示,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH…,如此下去,则第2017个正方形的边长是( )
如图所示,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH…,如此下去,则第2017个正方形的边长是( )
 如图所示,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH…,如此下去,则第2017个正方形的边长是( )
如图所示,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH…,如此下去,则第2017个正方形的边长是( )| A. | ${({\sqrt{2}})^{2016}}$ | B. | ${({\sqrt{2}})^{2017}}$ | C. | $2016\sqrt{2}$ | D. | $2017\sqrt{2}$ |
14.力帆集团原计划生产某一型号的汽车8000辆,为了提高效率,企业改进了技术,现每天可比原计划多生产40辆汽车,结果提前10天完成了生产计划.若设原计划需要x天完成,则根据题意列方程为( )
| A. | $\frac{8000}{x}$-$\frac{8000}{x+10}$=40 | B. | $\frac{8000}{x+10}$-$\frac{8000}{x}$=40 | ||
| C. | $\frac{8000}{x-10}$=$\frac{8000}{x}$+40 | D. | $\frac{8000}{x-10}$=$\frac{8000}{x}$-40 |
8.据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见表:若2015年5月份,该市居民甲用电100度,交电费60元.
(1)表中,a=0.6;若居民乙用电200度,则应交电费122.5元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度0.62元?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度但不超过300度的部分 | 0.65 |
| 超过300度的部分 | 0.9 |
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度0.62元?
9.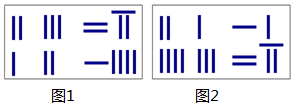 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )
 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )| A. | $\left\{\begin{array}{l}{2x+y=16}\\{4x+3y=22}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=16}\\{4x+3y=27}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=22}\end{array}\right.$ |