题目内容
15.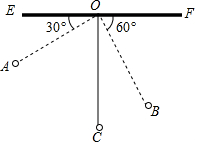 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:(1)单摆的长度($\sqrt{3}$≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
分析 (1)作AP⊥OC、BQ⊥OC,由题意得∠AOP=60°、∠BOQ=30°,设OA=OB=x,根据三角函数得OP=OAcos∠AOP=$\frac{1}{2}$x、OQ=OBcos∠BOQ=$\frac{\sqrt{3}}{2}$x,由PQ=OQ-OP可得关于x的方程,解之可得;
(2)由(1)知∠AOB=90°、OA=OB=7+7$\sqrt{3}$,利用弧长公式求解可得.
解答 解:(1)如图,过点A作AP⊥OC于点P,过点B作BQ⊥OC于点Q,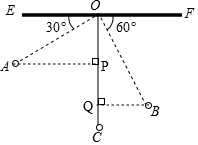
∵∠EOA=30°、∠FOB=60°,且OC⊥EF,
∴∠AOP=60°、∠BOQ=30°,
设OA=OB=x,
则在Rt△AOP中,OP=OAcos∠AOP=$\frac{1}{2}$x,
在Rt△BOQ中,OQ=OBcos∠BOQ=$\frac{\sqrt{3}}{2}$x,
由PQ=OQ-OP可得$\frac{\sqrt{3}}{2}$x-$\frac{1}{2}$x=7,
解得:x=7+7$\sqrt{3}$≈18.9(cm),
答:单摆的长度约为18.9cm;
(2)由(1)知,∠AOP=60°、∠BOQ=30°,且OA=OB=7+7$\sqrt{3}$,
∴∠AOB=90°,
则从点A摆动到点B经过的路径长为$\frac{90•π•(7+7\sqrt{3})}{180}$≈29.295,
答:从点A摆动到点B经过的路径长为29.295cm.
点评 本题主要考查解直角三角形的应用-仰角俯角问题,根据题意构建直角三角形,利用三角函数的定义表示出所需线段的长度及掌握弧长公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如果水位下降3m记作-3m,那么水位升高4m,记作( )
| A. | 1m | B. | 7m | C. | 4m | D. | -7m |
20.若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
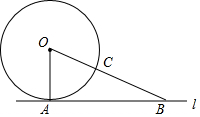 如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( ) 如图,DE⊥AB,EF∥AC,∠A=28°,求∠DEF的度数.
如图,DE⊥AB,EF∥AC,∠A=28°,求∠DEF的度数.