题目内容
7.若关于x、y的二元一次方程组$\left\{{\begin{array}{l}{x+y=3}\\{2x-ay=5}\end{array}}\right.$的解是$\left\{{\begin{array}{l}{x=b}\\{y=1}\end{array}}\right.$,则ab的值为1.分析 将方程组的解$\left\{{\begin{array}{l}{x=b}\\{y=1}\end{array}}\right.$代入方程组$\left\{{\begin{array}{l}{x+y=3}\\{2x-ay=5}\end{array}}\right.$,就可得到关于a、b的二元一次方程组,解得a、b的值,即可求ab的值.
解答 解:∵关于x、y的二元一次方程组$\left\{{\begin{array}{l}{x+y=3}\\{2x-ay=5}\end{array}}\right.$的解是$\left\{{\begin{array}{l}{x=b}\\{y=1}\end{array}}\right.$,
∴$\left\{\begin{array}{l}{b+1=3}\\{2b-a=5}\end{array}\right.$,
解得a=-1,b=2,
∴ab=(-1)2=1.
故答案为1.
点评 此题主要考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.也考查了解二元一次方程组.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
17.下列运算结果正确的是( )
| A. | a3+a4=a7 | B. | a4÷a3=a | C. | a3•a2=2a3 | D. | (a3)3=a6 |
2.若关于x的不等式x-$\frac{a}{2}$<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
12. 如图,直线a∥b,∠1=72°,则∠2的度数是( )
如图,直线a∥b,∠1=72°,则∠2的度数是( )
 如图,直线a∥b,∠1=72°,则∠2的度数是( )
如图,直线a∥b,∠1=72°,则∠2的度数是( )| A. | 118° | B. | 108° | C. | 98° | D. | 72° |
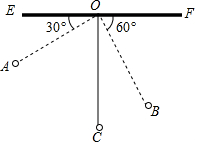 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: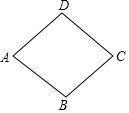 如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.
如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.