题目内容
4.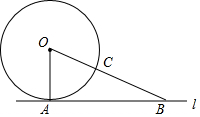 如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 根据勾股定理,可得OB的长,根据线段的和差,可得答案.
解答 解:由勾股定理,得
OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=13,
CB=OB-OC=13-5=8,
故选:D.
点评 本题考查了切线的性质,利用勾股定理得出OB的长是解题关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
14.下表为我省大同市5个空气质量监测站点对某日空气中PM2.5浓度(单位:μg/m3)的检测数据,则这组数据的中位数为( )
| 检测站点 | 果树杨 | 云冈宾馆 | 大同大学 | 安家小村 | 教育学院 |
| PM2.5浓度 | 76μg/m3 | 80μg/m3 | 97μg/m3 | 94μg/m3 | 93μg/m3 |
| A. | 97μg/m3 | B. | 80μg/m3 | C. | 94μg/m3 | D. | 93μg/m3 |
12. 如图,直线a∥b,∠1=72°,则∠2的度数是( )
如图,直线a∥b,∠1=72°,则∠2的度数是( )
 如图,直线a∥b,∠1=72°,则∠2的度数是( )
如图,直线a∥b,∠1=72°,则∠2的度数是( )| A. | 118° | B. | 108° | C. | 98° | D. | 72° |
4.我市某工艺厂为配合伦敦奥运,设计了一款成本为20元/件的工艺品投入市场进行试销,得到如数据:

(1)把表中x、y的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为9000元?(利润=销售总价-成本总价)
(3)根据要求,试销该工艺品每天获得的利润不低于8000元,每天销售量不低于350件,试确定销售单价x(元/件)的取值范围,并求出工艺厂试销该工艺品每天获得的最大利润.
| 销售单价x (元/件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量 y(件) | … | 500 | 400 | 300 | 200 | … |

(1)把表中x、y的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为9000元?(利润=销售总价-成本总价)
(3)根据要求,试销该工艺品每天获得的利润不低于8000元,每天销售量不低于350件,试确定销售单价x(元/件)的取值范围,并求出工艺厂试销该工艺品每天获得的最大利润.
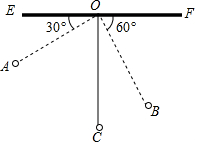 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: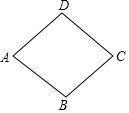 如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.
如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$. 如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为27cm,△BCE的周长为18cm,则AD的长为4.5cm.
如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为27cm,△BCE的周长为18cm,则AD的长为4.5cm.