题目内容
10.某新建成学校举行美化绿化校园活动,九年级计划购买A,B两种花木共100棵绿化操场,其中A花木每棵50元,B花木每棵100元.(1)若购进A,B两种花木刚好用去8000元,则购买了A,B两种花木各多少棵?
(2)如果购买B花木的数量不少于A花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用.
分析 (1)设购买A种花木x棵,B种花木y棵,根据“A,B两种花木共100棵、购进A,B两种花木刚好用去8000元”列方程组求解可得;
(2)设购买A种花木a棵,则购买B种花木(100-a)棵,根据“B花木的数量不少于A花木的数量”求得a的范围,再设购买总费用为W,列出W关于a的解析式,利用一次函数的性质求解可得.
解答 解:(1)设购买A种花木x棵,B种花木y棵,
根据题意,得:$\left\{\begin{array}{l}{x+y=100}\\{50x+100y=8000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=60}\end{array}\right.$,
答:购买A种花木40棵,B种花木60棵;
(2)设购买A种花木a棵,则购买B种花木(100-a)棵,
根据题意,得:100-a≥a,
解得:a≤50,
设购买总费用为W,
则W=50a+100(100-a)=-50a+10000,
∵W随a的增大而减小,
∴当a=50时,W取得最小值,最小值为7500元,
答:当购买A种花木50棵、B种花木50棵时,所需总费用最低,最低费用为7500元.
点评 本题主要考查二元一次方程组、一元一次不等式及一次函数的性质,理解题意找到题目蕴含的相等关系列出方程和函数解析式,熟练掌握一次函数性质是解题的关键.

练习册系列答案
相关题目
20. 下列哪一个是正立方体的展开图( )
下列哪一个是正立方体的展开图( )
 下列哪一个是正立方体的展开图( )
下列哪一个是正立方体的展开图( )| A. |  | B. |  | C. |  | D. |  |
1. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若关于x的不等式x-$\frac{a}{2}$<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
11. 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )| A. | 127° | B. | 53° | C. | 127°或53° | D. | 不能确定 |
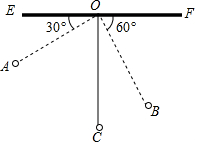 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: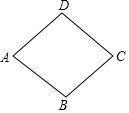 如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.
如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.