题目内容
16. 如图,DE⊥AB,EF∥AC,∠A=28°,求∠DEF的度数.
如图,DE⊥AB,EF∥AC,∠A=28°,求∠DEF的度数.
分析 先根据DE⊥AB可知∠ADE=90°,再由三角形内角和定理求出∠AGD的度数,根据平行线的性质即可得出结论.
解答 解:∵DE⊥AB,
∴∠EDA=90°,
∵∠EDA+∠A+∠AGD=180°,∠A=28°,
∴∠AGD=62°,
∴∠EGC=∠AGD=62°,
∵EF∥AC,
∴∠EGC+∠E=180°,
∴∠E=118°.
点评 本题考查的是平行线的性质及三角形内角和定理的运用,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.我市某工艺厂为配合伦敦奥运,设计了一款成本为20元/件的工艺品投入市场进行试销,得到如数据:

(1)把表中x、y的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为9000元?(利润=销售总价-成本总价)
(3)根据要求,试销该工艺品每天获得的利润不低于8000元,每天销售量不低于350件,试确定销售单价x(元/件)的取值范围,并求出工艺厂试销该工艺品每天获得的最大利润.
| 销售单价x (元/件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量 y(件) | … | 500 | 400 | 300 | 200 | … |

(1)把表中x、y的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为9000元?(利润=销售总价-成本总价)
(3)根据要求,试销该工艺品每天获得的利润不低于8000元,每天销售量不低于350件,试确定销售单价x(元/件)的取值范围,并求出工艺厂试销该工艺品每天获得的最大利润.
11. 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )| A. | 127° | B. | 53° | C. | 127°或53° | D. | 不能确定 |
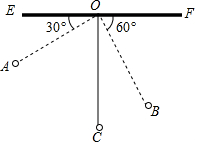 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: 如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为27cm,△BCE的周长为18cm,则AD的长为4.5cm.
如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为27cm,△BCE的周长为18cm,则AD的长为4.5cm. 如图,四边形ABCD中,AD∥BC,点E在边AB上,∠A=∠B=90°△ADE≌△BEC时,设AD=a,AE=b,DE=c,请利用如图,证明勾股定理:a2+b2=c2.
如图,四边形ABCD中,AD∥BC,点E在边AB上,∠A=∠B=90°△ADE≌△BEC时,设AD=a,AE=b,DE=c,请利用如图,证明勾股定理:a2+b2=c2.