题目内容
6.若关于x的分式方程$\frac{x}{x-2}$=2-$\frac{m}{2-x}$的解为正数,则满足条件的正整数m的值为1或3.分析 先根据分式方程的解法即求出x的表达式,然后根据题意求出m的范围即可求出答案.
解答 解:x=2(x-2)+m,
x=2x-4+m
x=4-m
将x=4-m代入x-2≠0,
∴m≠2
∵x>0
∴m<4,
∵m是正整数,
∴0<m<4且m≠2
∴m=1或3
故答案为:1或3
点评 本题考查分式方程的解法,解题的关键是求出m的范围,本题属于中等题型.

练习册系列答案
相关题目
17.下列运算结果正确的是( )
| A. | a3+a4=a7 | B. | a4÷a3=a | C. | a3•a2=2a3 | D. | (a3)3=a6 |
14.下表为我省大同市5个空气质量监测站点对某日空气中PM2.5浓度(单位:μg/m3)的检测数据,则这组数据的中位数为( )
| 检测站点 | 果树杨 | 云冈宾馆 | 大同大学 | 安家小村 | 教育学院 |
| PM2.5浓度 | 76μg/m3 | 80μg/m3 | 97μg/m3 | 94μg/m3 | 93μg/m3 |
| A. | 97μg/m3 | B. | 80μg/m3 | C. | 94μg/m3 | D. | 93μg/m3 |
 如图,⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点,则∠AOC的度数为144°.
如图,⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点,则∠AOC的度数为144°. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )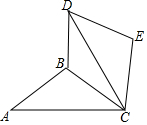 如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.
如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.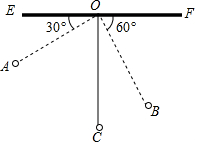 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: