题目内容
6．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD等于（ ）| A． | 32° | B． | 64° | C． | 128° | D． | 148° |
分析 根据圆内接四边形的性质得到∠A=∠DCE=64°，根据圆周角定理得到答案．
解答 解：∵四边形ABCD内接于⊙O，
∴∠A=∠DCE=64°，
∴∠BOD=2∠A=128°，
故选：C．
点评 本题考查的是圆内接四边形的性质和圆周角定理，掌握圆内接四边形的外角等于它的内对角是解题的关键．
练习册系列答案
相关题目
16．
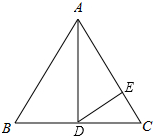如图，在△ABC中，AB=AC=13，AD为BC边上的中线，BC=10，DE⊥AC于点E，则tan∠CDE的值等于（ ）
如图，在△ABC中，AB=AC=13，AD为BC边上的中线，BC=10，DE⊥AC于点E，则tan∠CDE的值等于（ ）| A． | $\frac{5}{12}$ | B． | $\frac{12}{5}$ | C． | $\frac{5}{13}$ | D． | $\frac{10}{13}$ |
如图，有A、B、C三个小岛，B在A的北偏东85°，A岛在C岛的西南方向，B岛在C岛的南偏西20°方向，求∠ABC的度数．
11．数轴上表示整数的点称为整点，某数轴的单位长度为1cm，若在数轴上画出一条长2015cm的线段AB，则AB盖住的整点个数是（ ）
| A． | 2015或2016 | B． | 2014或2015 | C． | 2016 | D． | 2015 |
18．已知线段a=4，b=9，线段x是a，b的比例中项，则x等于（ ）
| A． | 6 | B． | 6或-6 | C． | -6 | D． | 36 |
16．某一动物细胞，细胞核与细胞壁之间的距离为0.0000075cm，用科学记数法表示为（ ）
| A． | 7.5×106cm | B． | 7.5×10-6cm | C． | 7.5×10-5cm | D． | -7.5×106cm |