题目内容
15．
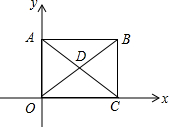已知，矩形ABCO的对角线AC、BO相交于点D，△ADO是等边三角形，且A点的坐标为（0，2），则点D的坐标为（$\sqrt{3}$，1）．
分析 作DH⊥OC于H．在Rt△DOH中，解直角三角形即可解决问题．
解答 解：作DH⊥OC于H．
∵△ADO是等边三角形，A（0，2），
∴OD=OA=2，∠AOD=60°，∠DOH=30°，
在Rt△ODH中，DH=$\frac{1}{2}$OD=1，OH=$\sqrt{3}$DH=$\sqrt{3}$，
∴D（$\sqrt{3}$，1），
故答案为（$\sqrt{3}$，1）．
点评 本题考查矩形的性质、等边三角形的性质、坐标与图形的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
练习册系列答案
互动英语系列答案
相关题目
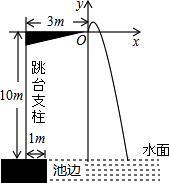如图，2016年里约奥运会上，某运动员在10米跳台跳水比赛时估测身体（看成一点）在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x（图中标出的数据为已知条件），运动员在空中运动的最大高度离水面为$10\frac{2}{3}$米．
6．下列计算正确的是（ ）
| A． | 3$\sqrt{3}$×5$\sqrt{3}$=15$\sqrt{3}$ | B． | 3$\sqrt{2}$$+2\sqrt{3}$=5$\sqrt{6}$ | C． | $\sqrt{8}$$-\sqrt{6}$=$\sqrt{2}$ | D． | $\sqrt{60}$$÷\sqrt{5}$=2$\sqrt{3}$ |
