题目内容
20．平面内有不重合的4条直线，请指出这4条直线交点个数的所有情况，并画出相应的草图．分析 从平行线的角度考虑，先考虑四条直线都平行，再考虑三条、两条直至都不平行，作出草图即可看出．
解答 解：（1）当四条直线平行时，无交点，
（2）当三条平行，另一条与这三条不平行时，有3个交点，
（3）当两两直线平行时，有4个交点，
（4）当有两条直线平行，而另两条不平行时，有5个交点，
（5）当四条直线同交于一点时，只有1个交点，
（6）当四条直线两两相交，且不过同一点时，有6个交点，
（7）当有两条直线平行，而另两条不平行并且交点在平行线上时，有3个交点，
（8）当三条直线交于一点，第四条直线与其它三条直线有三个交点时，共有4个交点，
故4条直线交点个数为：0或1或3或4或5或6．
点评 本题考查了平行线与相交线的位置关系，没有明确平面上四条不重合直线的位置关系，需要运用分类讨论思想，从四条直线都平行线，然后数量上依次递减，直至都不平行，这样可以做到不重不漏，准确找出所有答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B、C，点A的坐标是（-$\sqrt{3}$，0），另一条直线经过点A、C．
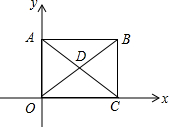已知，矩形ABCO的对角线AC、BO相交于点D，△ADO是等边三角形，且A点的坐标为（0，2），则点D的坐标为（$\sqrt{3}$，1）．
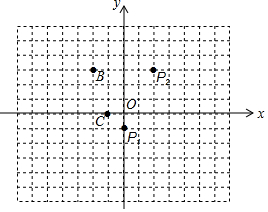阅读理解：我们知道，任意两点关于它们所连线段的中点成中心对称，在平面直角坐标系中，任意两点P（x1，y1）、Q（x2，y2）的对称中心的坐标为（$\frac{{x}_{1}+{x}_{2}}{2}$，$\frac{{y}_{1}+{y}_{2}}{2}$）．
12．
我国著名的数学家华罗庚曾说过：“数形结合百般好，割裂分家万事非”，如图：在边长为1的正方形纸板上，依次贴上面积为$\frac{1}{2}$，$\frac{1}{4}$，$\frac{1}{8}$，…，$\frac{1}{{2}^{n}}$的长方形彩色纸片（n为大于1的整数），请你用“数形结合”的思想，依数形变化的规律，计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=（ ）
我国著名的数学家华罗庚曾说过：“数形结合百般好，割裂分家万事非”，如图：在边长为1的正方形纸板上，依次贴上面积为$\frac{1}{2}$，$\frac{1}{4}$，$\frac{1}{8}$，…，$\frac{1}{{2}^{n}}$的长方形彩色纸片（n为大于1的整数），请你用“数形结合”的思想，依数形变化的规律，计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=（ ）| A． | $\frac{9}{8}$ | B． | $\frac{5}{4}$ | C． | $\frac{17}{16}$ | D． | 1-$\frac{1}{{2}^{n}}$ |
如图，比例规是一种画图工具，它由长度相等的两脚AC和BD交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC，OB=3OD），然后张开两脚，使A，B两个尖端分别在线段a的两个端点上，当CD=1.8cm时，则AB的长为（ ）