题目内容
4.若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m,n(m<n),方程x2+ax+b=2有两个不同的实数根p,q(p<q),则m,n,p,q的大小关系用“<”连接为p<m<n<q.分析 首先画出y=x2+ax+b和y=2的图象,然后结合图象选择正确答案即可.
解答 解:函数y=x2+ax+b如图所示:
结合图象可知:p<m<n<q.
故答案为:p<m<n<q.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是作出抛物线的图象,数形结合进行答题.

练习册系列答案
相关题目
12. 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图:在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=( )
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图:在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=( )
 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图:在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=( )
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图:在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=( )| A. | $\frac{9}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{17}{16}$ | D. | 1-$\frac{1}{{2}^{n}}$ |
19.为了打造区域中心城市,实现跨越式发展,我市新区建设正按投资计划有序推进.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型挖掘机 | 100 | 60 |
| 乙型挖掘机 | 120 | 80 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
9. 如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
 如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )| A. | 7.2 cm | B. | 5.4 cm | C. | 3.6 cm | D. | 0.6 cm |
18.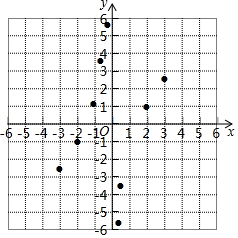 有这样一个问题:探究函数y=x-$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=x-$\frac{2}{x}$的图象和性质.
小石根据学习函数的经验,对此函数的图象和性质进行了探究.
下面是小石的探究过程,请补充完整:
(1)函数的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出此函数的图象;
(4)进一步探究,结合函数的图象,写出此函数的性质(一条即可):当x<0时,y随x的增大而增大;当x>0时,y随x的增大而增大.
 有这样一个问题:探究函数y=x-$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=x-$\frac{2}{x}$的图象和性质.小石根据学习函数的经验,对此函数的图象和性质进行了探究.
下面是小石的探究过程,请补充完整:
(1)函数的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{7}{3}$ | -1 | 1 | $\frac{7}{2}$ | $\frac{17}{3}$ | -$\frac{17}{3}$ | -$\frac{7}{2}$ | m | 1 | $\frac{7}{3}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出此函数的图象;
(4)进一步探究,结合函数的图象,写出此函数的性质(一条即可):当x<0时,y随x的增大而增大;当x>0时,y随x的增大而增大.
19.在△ABC中,AB=AC,如果AB边上的高等于AB的一半,那么∠A的度数为( )
| A. | 150° | B. | 150°和45° | C. | 30° | D. | 150°和30° |
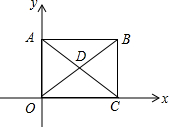 已知,矩形ABCO的对角线AC、BO相交于点D,△ADO是等边三角形,且A点的坐标为(0,2),则点D的坐标为($\sqrt{3}$,1).
已知,矩形ABCO的对角线AC、BO相交于点D,△ADO是等边三角形,且A点的坐标为(0,2),则点D的坐标为($\sqrt{3}$,1).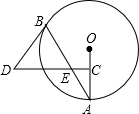 如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.