题目内容
17.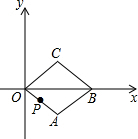 如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
分析 根据旋转的性质得出每6秒一个循环,点P在菱形的边上4秒一个循环,利用点P的坐标的规律进行解答即可.
解答 解:当运动时间为1秒时,菱形边OC在y的正半轴上,此时点P运动到A点,点A在第一象限,
所以点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);
因为第2秒点P运动到B处,此时点P在第二象限坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$);
第3秒点P运动到C处,此时点P在第三象限坐标为(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$);
第4秒点P运动到O处,此时点P的坐标为(0,0);
第5秒点P运动到A处,此时点P在第四象限坐标为($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$);
第6秒点P运动到B处,此时点P在第一象限坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$);
所以2015÷4=503…3,2015÷6=370…5,
所以点P与点C重合在第四象限,坐标为($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$),
故答案为:($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$)
点评 此题考查旋转与坐标,关键是根据旋转的性质得出旋转的规律.

练习册系列答案
相关题目
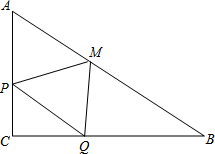 在Rt△ABC中,∠C=90°,AC=6,BC=8,直线PQ沿CA方向自C向A运动,速度为1cm/s,且总保持PQ∥AB;同时,点M从A出发沿AB方向向B运动,速度为2cm/s.设运动时间为t(0<t<4)
在Rt△ABC中,∠C=90°,AC=6,BC=8,直线PQ沿CA方向自C向A运动,速度为1cm/s,且总保持PQ∥AB;同时,点M从A出发沿AB方向向B运动,速度为2cm/s.设运动时间为t(0<t<4)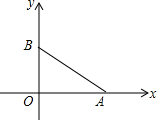 如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).
如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).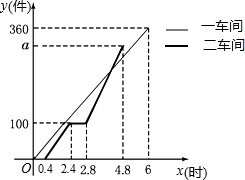 某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:
某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示: 如图,矩形ABCD中,点E、F在边AD上,AF=DE,求证:BE=CF.
如图,矩形ABCD中,点E、F在边AD上,AF=DE,求证:BE=CF.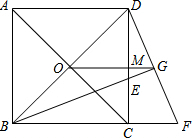 已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.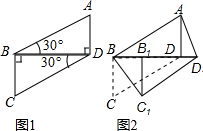 将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).
将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).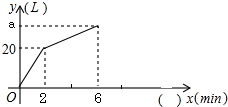 一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.
一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.