题目内容
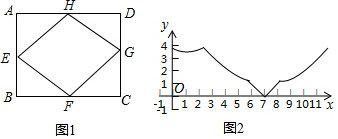
9. 如图,矩形ABCD中,BC=2AB=3,DE=2EC,∠EAF=45°,则BF的长为0.75.
如图,矩形ABCD中,BC=2AB=3,DE=2EC,∠EAF=45°,则BF的长为0.75.
分析 先构造正方形ADQP,根据∠EAF=45°得到△GAE≌△GAH(SAS),进而得出HG=EG,设PG=x,则GH=1+x=GE,GQ=3-x,在Rt△EGQ中,根据EQ2+GQ2=GE2,可得方程22+(3-x)2=(1+x)2,即可得出PG=1.5,最后根据BF∥PG,B为AP的中点,即可得到BF的长.
解答  解:如图所示,延长AB至P,使得BP=AB,延长DC至Q,使得CQ=DC,连接PQ,则四边形ADQP是正方形,
解:如图所示,延长AB至P,使得BP=AB,延长DC至Q,使得CQ=DC,连接PQ,则四边形ADQP是正方形,
延长AF交PQ于G,连接GE,将△ADE绕着点A顺时针旋转90°得△APH,则H,P,G在同一直线上,AE=AH,
∵∠GAE=45°,∠DAP=90°,
∴∠PAH+∠PAG=∠DAE+∠PAG=45°,
∴∠GAE=∠GAH,
在△GAE和△GAH中,
$\left\{\begin{array}{l}{AE=AH}\\{∠GAE=∠GAH}\\{AG=AG}\end{array}\right.$,
∴△GAE≌△GAH(SAS),
∴HG=EG,
由题可得,DE=1=HP,EC=0.5,CQ=1.5,PQ=3,
设PG=x,则GH=1+x=GE,GQ=3-x,
在Rt△EGQ中,EQ2+GQ2=GE2,
即22+(3-x)2=(1+x)2,
解得x=1.5,
∴PG=1.5,
∵BF∥PG,B为AP的中点,
∴$\frac{AB}{AP}$=$\frac{BF}{PG}$=$\frac{1}{2}$,
∴BF=$\frac{1}{2}$PG=0.75,
故答案为:0.75
点评 本题主要考查了矩形的性质,正方形的性质,全等三角形的判定与性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造全等三角形以及正方形,依据勾股定理列方程进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列计算正确的是( )
| A. | (a+2)(a-2)=a2-2 | B. | (a+1)(a-2)=a2+a-2 | C. | (a+b)2=a2+b2 | D. | (a-b)2=a2-2ab+b2 |
17.为了奖励在艺术节活动中表现突出的同学,七(1)班班主任曾两次到多福居给同学们买牛奶和面包,具体数量与金额如表所示:
(1)求牛奶和面包的单价分别是多少元?
(2)该店某天开展优惠促销活动:牛奶每箱6瓶,每买1箱送1瓶;面包全场八折,假设牛奶只能整箱购买.七(1)班共有56名学生.
①若要使每名学生各分得牛奶1瓶和面包1个,共需要多少元钱?
②若要使每名学生至少分得1瓶牛奶和1个面包,共花费560元,求购买的牛奶是多少瓶?面包是多少个?
| 次数 | 牛奶(瓶) | 面包(个) | 总金额(元) |
| 第1次 | 30 | 50 | 430 |
| 第2次 | 20 | 60 | 420 |
(2)该店某天开展优惠促销活动:牛奶每箱6瓶,每买1箱送1瓶;面包全场八折,假设牛奶只能整箱购买.七(1)班共有56名学生.
①若要使每名学生各分得牛奶1瓶和面包1个,共需要多少元钱?
②若要使每名学生至少分得1瓶牛奶和1个面包,共花费560元,求购买的牛奶是多少瓶?面包是多少个?
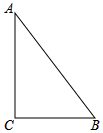 如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.
如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.