Question

14．如图，将△ABC绕点A逆时针旋转，使B到D，C到E，点D恰好在BC边上，且BD=4DC=4，DE交AC于F，已知△ABC的面积为10．
（1）求证：AE∥BC；
（2）求△ADF的面积．

Answer 1

分析 （1）过A作AH⊥BC于H，由旋转的性质得到AB=AD，∠BAC=∠DAE，根据等腰三角形的性质得到BH=DH=$\frac{1}{2}$BD=2，∠BAD=∠CAE，由三角形的面积达到AH=4，根据勾股定理得到AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=5，根据相似三角形的性质得到∠BAD=∠ACB，根据平行线的判定即可得到结论；
（2）由BD=4DC，得到S_△ACD=$\frac{1}{5}$S_△ABC=2，根据相似三角形的性质得到$\frac{AF}{CF}$=$\frac{AE}{CD}$=$\frac{5}{1}$，求得$\frac{AF}{AC}$=$\frac{5}{6}$，于是得到结论．

解答 解：（1）过A作AH⊥BC于H，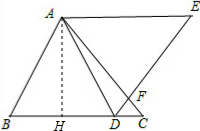
∵将△ABC绕点A逆时针旋转，使B到D，C到E，点D恰好在BC边上，
∴AB=AD，∠BAC=∠DAE，
∴BH=DH=$\frac{1}{2}$BD=2，
∴∠BAD=∠CAE，
∵BD=4DC=4，
∴CD=1，
∴BC=5，CH=3，
∵△ABC的面积为10，
∴AH=4，
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=5，
∴AC=BC，
∴△ABD与△ABC是等腰三角形，
∵∠B=∠B，
∴△ABC∽△ABD，
∴∠BAD=∠ACB，
∴∠CAE=∠C，
∴AE∥BC；

（2）∵BD=4DC，
∴S_△ACD=$\frac{1}{5}$S_△ABC=2，
∵AE∥BC，
∴△CDF∽△AEF，
∴$\frac{AF}{CF}$=$\frac{AE}{CD}$=$\frac{5}{1}$，
∴$\frac{AF}{AC}$=$\frac{5}{6}$，
∴S_△ADF=$\frac{5}{6}$S_△ADC=$\frac{5}{3}$．

点评 本题考查了旋转的性质，相似三角形的判定和性质，三角形面积的计算，等腰三角形的性质，平行线的判定，正确的作出辅助线是解题的关键．