题目内容
6.将面积为4的正方形ABCD与面积为8的正方形AEFG按图①的位置放置,AD、AE在同一条直线上,AB、AG在同一条直线上.(1)试判断DG、BE的数量和位置关系,并说明理由;
(2)如图2,将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,求此时BE的长;
(3)如图3,将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,请直接写出△GHE与△BHD面积之和的最大值.
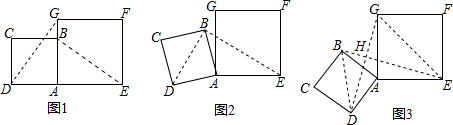
分析 (1)由正方形的性质可证△ADG≌△ABE(SAS),因此可证得∠AGD=∠AEB,如图1,延长EB交DG于点H,然后由三角形的内角和和直角三角形的两锐角互余可证得结论;由正方形的性质和等量代换可证△ADG≌△ABE(SAS),因此可证得DG=BE,
(2)如图2,过点A作AM⊥DG交DG于点M,根据正方形的性质可证得DM=AM=$\sqrt{2}$,然后根据勾股定理可求得GM的长,进而可求得BE=DG=DM+GM.
(3)对于△EGH,点H在以EG为直径的圆上,所以当点H与点A重合时,△EGH的高最大,对于△BDH,点H在以BD为直径的圆上,所以当点H与点A重合时,△BDH的高最大,因此求出这时的面积,再相加即可.
解答 解:(1)DG=BE,DG⊥BE,如图1,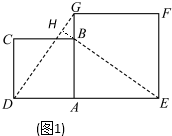
四边形ABCD与四边形AEFG是正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE,
∴△ADG≌△ABE(SAS),
∴DG=BE,∠AGD=∠AEB,
延长EB交DG于点H,
△ADG中∠AGD+∠ADG=90°,
∴∠AEB+∠ADG=90°,
△DEH中,∠AEB+∠ADG+∠DHE=180°,
∴∠DHE=90°,
∴DG⊥BE,
∴DG=BE,DG⊥BE;
(2)四边形ABCD与四边形AEFG是正方形,
∴AD=AB,∠DAB=∠GAE=90°,AG=AE,
∴∠DAB+∠BAG=∠GAE+∠BAG,
∴∠DAG=∠BAE,
AD=AB,∠DAG=∠BAE,AG=AE,
∴△ADG≌△ABE(SAS),
∴DG=BE,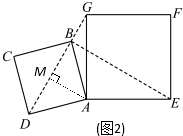
如图2,过点A作AM⊥DG交DG于点M,
∠AMD=∠AMG=90°
BD是正方形ABCD的对角线,
∴∠MDA=45°,
∵面积为4的正方形ABCD与面积为8的正方形AEFG
∴AD=2,AE=2$\sqrt{2}$,
在Rt△AMD中,∠MDA=45°,
∴cos45°=$\frac{DM}{AD}$,
∴DM=$\sqrt{2}$,
∴AM=$\sqrt{2}$,
在Rt△AMG中,GM=$\sqrt{A{G}^{2}-A{M}^{2}}$=$\sqrt{6}$,
∵DG=DM+GM=$\sqrt{2}$+$\sqrt{6}$,
∴BE=DG=$\sqrt{2}$+$\sqrt{6}$,
(3)面积的最大值为6.
如图,
对于△EGH,点H在以EG为直径的圆上,
所以当点H与点A重合时,△EGH的高最大,
∴S△EGH=$\frac{1}{2}$AG×AE=$\frac{1}{2}$×8=4,
对于△BDH,点H在以BD为直径的圆上,
所以当点H与点A重合时,△BDH的高最大,
∴S△BDH=$\frac{1}{2}$AD×AB=$\frac{1}{2}$×4=2,
∴△GHE与△BHD面积之和的最大值是4+2=6.
点评 此题是四边形综合题,主要考查了正方形的性质,锐角三角函数,全等三角形的性质和判定,解本题的关键是锐角三角函数的灵活运用.


 如图,是将一个长方体沿它的对角线切去一半后剩下的部分.
如图,是将一个长方体沿它的对角线切去一半后剩下的部分.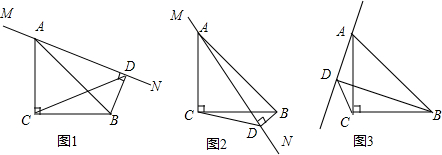
 如图,将△ABC绕点A逆时针旋转,使B到D,C到E,点D恰好在BC边上,且BD=4DC=4,DE交AC于F,已知△ABC的面积为10.
如图,将△ABC绕点A逆时针旋转,使B到D,C到E,点D恰好在BC边上,且BD=4DC=4,DE交AC于F,已知△ABC的面积为10.