题目内容
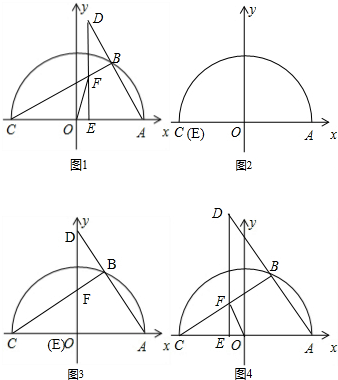
8.如图1,在平面直角坐标系中,点A(5,0),以OA为半径作半圆O交x轴于点C,点B是该半圆上一动点,连结CB、AB,并延长AB至点D,使DB=AB,过点D作DE⊥x轴于点E,直线DE与BC交于点F,连结OF.(1)当点E与点C重合时,①请在图2中画出图形,此时直线CD与⊙O的位置关系是CD与⊙O相切.②求线段AB的长.
(2)当点E与点O重合时(如图3所示),求点D的坐标.
(3)当点E的坐标为(1,0)时,求线段EF的长.
(4)如图4,在点B运动过程中,若点E位于O、C之间时,是否存在以点E、O、F为顶点的三角形与△ACB相似,若存在,请直接写出此时点E的坐标;若不存在,请说明理由.
分析 (1)先判断出CB是AD的垂直平分线,再由勾股定理计算即可;
(2)先求出∠DAO=60°,然后用锐角三角函数计算即可;
(3)先利用勾股定理计算出DE,在判断出△CEF∽△DEA,利用比例式计算;
(4)分两种情况计算①当∠EOF=∠A时,用$\frac{OF}{AD}=\frac{OE}{AE}$=$\frac{1}{4}$计算,②当∠EOF=∠ABC时,和前面方法也一样.
解答 解:(1)①作图如图2所示,
∵DE⊥x,AC为⊙O的直径,
∴直线CD与⊙O相切,
②∵AC是⊙O的直径,
∴∠CBA=90°,
∵DB=AB,
∴CB是AD的垂直平分线,
∴DC=AC=10,
根据勾股定理得,AD=$\sqrt{A{C}^{2}+D{C}^{2}}$=10$\sqrt{2}$,
∴AB=5$\sqrt{2}$;
(2)如图3,
点E,O重合时,点D落在y轴上,连接OB,
∵∠AOD=90°,DB=AB,
∴OB=$\frac{1}{2}$AD=AB=OA,
∴∠DAO=60°,
在Rt△AOD中,OD=OAtan∠DAO=5tan60°=5$\sqrt{3}$,
∴D(0,5$\sqrt{3}$),
(3)如图4,连接CD,
同(1)②的方法一样,可得CD=CA=10,
当点E坐标为(1,0)时,
CE=OC+OE=6,AE=OA-OE=4,
在Rt△CED中,DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=8,
∵∠ACB=90°-∠CAB=∠ADE,∠CEF=∠DEA,
∴△CEF∽△DEA,
∴$\frac{EF}{EA}=\frac{CE}{DE}$,
∴$\frac{EF}{4}=\frac{6}{8}$,
∴EF=3;
(4)当∠EOF=∠A,则OF∥BD,
∴OF=$\frac{1}{2}$BC=$\frac{1}{4}$BD,
∴$\frac{OF}{BD}=\frac{OE}{BE}$=$\frac{1}{4}$,
∴$\frac{-x}{5-x}=\frac{1}{4}$,
∴x=-$\frac{5}{3}$,
∴E(-$\frac{5}{3}$,0),
当∠EOF=∠ABC,同理可得x=-$\frac{5}{2}$,
∴E(-$\frac{5}{2}$,0);
即:E(-$\frac{5}{3}$,0)或E(-$\frac{5}{2}$,0);
点评 本题是圆的综合题,考查了相似三角形的判定与性质,勾股定理的运用,圆周角定理,关键是理解题意,根据基本条件,图形的性质,分类求解.

| A. | -a3 | B. | -a6 | C. | -a9 | D. | a9 |
 如图,小明从点O出发,沿直线前进10米后向左转n°(0<n<90),再沿直线前进10米向左转相同的度数,…照这样走下去,小明发现:当他第一次回到了出发点时,共转过了24次,则小明每次转过的角度n的值为( )
如图,小明从点O出发,沿直线前进10米后向左转n°(0<n<90),再沿直线前进10米向左转相同的度数,…照这样走下去,小明发现:当他第一次回到了出发点时,共转过了24次,则小明每次转过的角度n的值为( )| A. | $14\frac{2}{5}$ | B. | 15 | C. | $15\frac{15}{23}$ | D. | 36 |
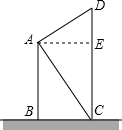 小华家与小丽家的两楼相邻,且相距10米,如图,小华家的楼高AB为18米;从小华家楼的顶部目测小丽家住的楼房CD的底部与顶部,视线与水平线的夹角分别为55°和35°,你能否求出小丽家住的楼房CD有多高?请说明理由.
小华家与小丽家的两楼相邻,且相距10米,如图,小华家的楼高AB为18米;从小华家楼的顶部目测小丽家住的楼房CD的底部与顶部,视线与水平线的夹角分别为55°和35°,你能否求出小丽家住的楼房CD有多高?请说明理由.