题目内容
18.用配方法将下列各式化为a(x+h)2+k的形式:(1)x2+5x-1;(2)2x2-x+3.
分析 (1)原式将-1变形为$\frac{25}{4}$-$\frac{29}{4}$,利用完全平方公式变形即可得到结果;
(2)原式前两项提取2,再利用完全平方公式配方即可得到结果.
解答 解:(1)原式=x2+5x+$\frac{25}{4}$-$\frac{29}{4}$=(x+$\frac{5}{2}$)2-$\frac{29}{4}$;
(2)原式=2(x2-$\frac{1}{2}$x+$\frac{1}{16}$)+3-$\frac{1}{8}$=2(x-$\frac{1}{4}$)2+$\frac{23}{8}$.
点评 此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.a6÷a3结果是( )
| A. | a3 | B. | a2 | C. | a9 | D. | a-3 |
13.下列计算正确的是( )
| A. | 2a2+a2=3a4 | B. | a2-a=a | C. | a2•a3=a5 | D. | a6÷a3=a2 |
3.下列计算正确的是( )
| A. | 2x+1=2x2 | B. | x2•x3=x5 | C. | (x2)3=x5 | D. | (2x)3=2x3 |
7.下列计算中,正确的是( )
| A. | -a(3a2-1)=-3a3-a | B. | (-2a-3)(2a-3)=9-4a2 | ||
| C. | (2+x)(x-2)=4-x2 | D. | (ab-c)(-c+ab)=a2b2-c2 |
8.(-x4)3等于( )
| A. | x7 | B. | x12 | C. | -x7 | D. | -x12 |
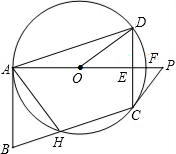 如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.