题目内容
8. 某班50名同学分别站在同一公路上相距1000米的M、N两点处,M处有30人,N处有20人,要让两处的同学集合到一起,并且使所有同学走的路程总和最小,那么集合地点应选在( )
某班50名同学分别站在同一公路上相距1000米的M、N两点处,M处有30人,N处有20人,要让两处的同学集合到一起,并且使所有同学走的路程总和最小,那么集合地点应选在( )| A. | M点处 | B. | N点处 | ||
| C. | 线段MN的中点处 | D. | 线段MN上,距M点400米处 |
分析 设M处学生走的路程,表示出N处学生走的路程,然后列式计算所有同学走的路程之和.
解答 解:设M处的同学走x米,那么N处的同学走(1000-x)米,
所有同学走的路程总和:
L=30x+20(1000-x)=10x+20000
此时0≤x≤1000,要使L最小,必须x=0,
此时L最小值为20000;
所以选M点处.
故选A.
点评 此题主要考查一次函数在实际生活中的意义,解决本题的关键是列出函数关系式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,镜子中号码的实际号码是( )
如图,镜子中号码的实际号码是( )
 如图,镜子中号码的实际号码是( )
如图,镜子中号码的实际号码是( )| A. | 2653 | B. | 3562 | C. | 3265 | D. | 5623 |
 如图,△ABC与△A′B′C′关于直线l对称,若∠A=50°,∠C′=25°,则∠B的度数为105°.
如图,△ABC与△A′B′C′关于直线l对称,若∠A=50°,∠C′=25°,则∠B的度数为105°. 如图,是一个正方体表面展开图,请在图中空格内填上适当的数,使这个正方体相对两个面上标注的数值相等(将答案填在图中空格内)
如图,是一个正方体表面展开图,请在图中空格内填上适当的数,使这个正方体相对两个面上标注的数值相等(将答案填在图中空格内) 如图,AD是∠BAC的平分线,点E在BC上,点F在CA的延长线上,EF∥AD交AB于点G,那么图中与∠F相等的角的个数有( )
如图,AD是∠BAC的平分线,点E在BC上,点F在CA的延长线上,EF∥AD交AB于点G,那么图中与∠F相等的角的个数有( )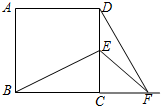 已知,如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.
已知,如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.