题目内容
17. 如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.
如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.
分析 根据角平分线的定义及三角形的外角性质可表示出∠A与∠D,从而不难发现两者的数量关系,进一步得出答案即可.
解答 解:∵∠ABC的平分线交∠ACE的外角平分线∠ACE的平分线于点D,
∴∠ABC=2∠DBC,∠ACE=2∠DCE,
∵∠DCE是△BCD的外角,
∴∠D=∠DCE-∠DBE,
∵∠ACE是△ABC的外角,
∠A=∠ACE-∠ABC=2∠DCE-2∠DBE=2(∠DCE-∠DBE),
∴∠A=2∠D.
点评 此题主要考查角平分线的意义以及三角形的外角的性质:三角形的一个外角等于和它不相邻的两个内角的和,解决本题的关键是三角形外角的性质.

练习册系列答案
相关题目
12.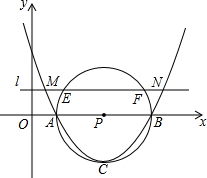 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{2}$ | C. | 5 | D. | 6 |
7.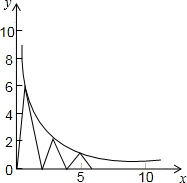 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )| A. | $\frac{6}{2n-1}$ | B. | $\frac{6}{{2}^{n+1}}$ | C. | $\frac{6}{2n+1}$ | D. | $\frac{6}{{2}^{n-1}}$ |
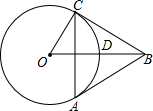 如图,⊙O的半径为2,OB=4,OB交⊙O于点D,点C是⊙O上一动点,以BC为边向下作等边△ABC.
如图,⊙O的半径为2,OB=4,OB交⊙O于点D,点C是⊙O上一动点,以BC为边向下作等边△ABC. 如图是由五块积木搭成的,这几块积木都是相同的正方体,请你画出从这个图形的正面看、上面看、左面看的平面图.
如图是由五块积木搭成的,这几块积木都是相同的正方体,请你画出从这个图形的正面看、上面看、左面看的平面图.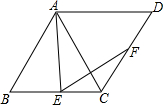 如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.
如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.